Question

19．如图，在菱形ABCD中，AD=2，点E在BC边上，将菱形ABCD沿直线AE折叠，点B恰巧落在AC上的点B′处，连接BE′，若BE′⊥BC，则AE=$\sqrt{6}$．

Answer 1

分析 过A作AF⊥CB交CB 的延长线于F，由折叠的性质得到∠1=∠2，∠3=∠4，根据垂直的定义得到∠B′EB=90°，得到∠1=∠2=45°，根据菱形的性质得到∠5=∠CAB，根据三角形的外角的性质得到∠3=∠4=15°，得到∠5=30°，解直角三角形即刻得到结论．

解答 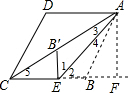解：过A作AF⊥CB交CB 的延长线于F，
∵△AB′E是△ABE沿着AE折叠得到的，
∴∠1=∠2，∠3=∠4，
∵BE′⊥BC，
∴∠B′EB=90°，
∴∠1=∠2=45°，
∵四边形ABCD是菱形，
∴∠5=∠CAB，
∴∠5=2∠2，
∵∠3+∠5=∠2，
∴∠2=3∠3，
∴∠3=∠4=15°，
∴∠5=30°，
∴∠ABF=60°，
∵AB=2，∠F=90°，
∴AF=$\sqrt{3}$，
∴AE=$\sqrt{2}$AF=$\sqrt{6}$．
故答案为：$\sqrt{6}$．

点评 本题考查了翻折变换（折叠问题），菱形的性质，解直角三角形，正确的作出辅助线是解题的关键．