题目内容
12．
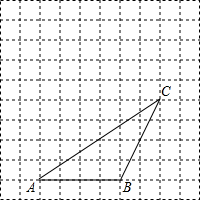如图，网格中每个小正方形边长为1，△ABC的顶点都在格点上．将△ABC向左平移2格，再向上平移3格，得到△A′B′C′．（1）请在图中画出平移后的△A′B′C′；
（2）画出平移后的△A′B′C′的中线B′D′
（3）若连接BB′，CC′，则这两条线段的关系是BB′∥CC′，BB′=CC′
（4）△ABC在整个平移过程中线段AB扫过的面积为12
（5）若△ABC与△ABE面积相等，则图中满足条件且异于点C的格点E共有10个
（注：格点指网格线的交点）
分析 （1）利用网格特点和平移的性质画出A、B、C的对应点A′、B′、C′即可；
（2）利用网格特点找出A′C′的中点D′，然后连接B′D′即可；
（3）根据平移的性质求解；
（4）利用平移的性质和平行四边形的面积公式求解；
（5）过点C作AB的平行线，然后找出此平行线上的格点即可．
解答 解：（1）如图，△A′B′C′为所作；
（2）如图，中线B′D′为所作；
（3）BB′∥CC′，BB′=CC′；
（4）△ABC在整个平移过程中线段AB扫过的面积=4×3=12；
（5）满足条件且异于点C的格点E共有10个．
故答案为BB′∥CC′，BB′=CC′；12；10．
点评 本题考查了作图-平移变换：确定平移后图形的基本要素有两个：平移方向、平移距离．作图时要先找到图形的关键点，分别把这几个关键点按照平移的方向和距离确定对应点后，再顺次连接对应点即可得到平移后的图形．
练习册系列答案
相关题目
如图，在△ABC中，AD⊥BC，AE平分∠BAC，∠B=70°，∠C=30°．
画图并填空：如图，每个小正方形的边长为1个单位，每个小正方形的顶点叫格点．
1．如图1，将边长为1的正方形ABCD压扁为边长为1的菱形ABCD．在菱形ABCD中，∠A的大小为α，面积记为S．
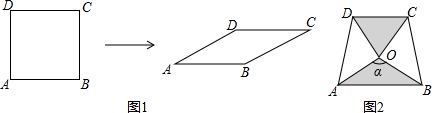
（1）请补全表：
（2）填空：由（1）可以发现单位正方形在压扁的过程中，菱形的面积随着∠A大小的变化而变化，不妨把单位菱形的面积S记为S（α）．例如：当α=30°时，S=S（30°）=$\frac{1}{2}$；当α=135°时，S=S=$\frac{\sqrt{2}}{2}$．由上表可以得到S（60°）=S（120°）；S（30°）=S（30°），…，由此可以归纳出S（α）=（α°）．
（3）两块相同的等腰直角三角板按图2的方式放置，AD=$\sqrt{2}$，∠AOB=α，试探究图中两个带阴影的三角形面积是否相等，并说明理由（注：可以利用（2）中的结论）．
（1）请补全表：
| α | 30° | 45° | 60° | 90° | 120° | 135° | 150° |
| S | $\frac{1}{2}$ | 1 | $\frac{\sqrt{2}}{2}$ |
（3）两块相同的等腰直角三角板按图2的方式放置，AD=$\sqrt{2}$，∠AOB=α，试探究图中两个带阴影的三角形面积是否相等，并说明理由（注：可以利用（2）中的结论）．