题目内容
13.某商人发现行驶在道路上的汽车越来越多,估计相应的汽车配套用品会畅销,于是决定购进A、B两种汽车配套用品,经调查,A种汽车配套用品每套进价比B种贵25元,购进A种汽车配套用品6套和B种汽车配套用品4套共用900元.(1)求A、B两种汽车配套用品的进价各是多少元?
(2)根据市场需求,商人决定购进 B种汽车配套用品的数量是购进 A种汽车配套用品的2倍还多4套,若A种汽车配套用品的售价为140元,B种汽车配套用品的售价为105元,且这批汽车配套用品全部售出后,利润超过1620元,那么购进A种汽车配套用品的数量至少多少套?
分析 (1)设A种汽车配套用品的进价是x元,B种汽车配套用品的进价是y元.根据“A种汽车配套用品每套进价比B种贵25元,购进A种汽车配套用品6套和B种汽车配套用品4套共用900元”列出方程组并解答即可;
(2)设购进A种汽车配套用品的数量是a套,根据题意列出不等式并解答即可.
解答 解:(1)设A种汽车配套用品的进价是x元,B种汽车配套用品的进价是y元,
依题意得:$\left\{\begin{array}{l}{x-y=25}\\{6x+4y=900}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=100}\\{y=75}\end{array}\right.$.
答:A种汽车配套用品的进价是100元,B种汽车配套用品的进价是75元;
(2)设购进A种汽车配套用品的数量是a套,则购进B种汽车配套用品的数量是(2a+4)套,
依题意得:(140-100)a+(105-75)(2a+4)>1620,
解得a>13.8.
答:购进A种汽车配套用品的数量至少14套.
点评 本题考查了一元一次不等式和二元一次方程组的应用.解决问题的关键是读懂题意,找到关键描述语,找到所求的量的数量关系.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
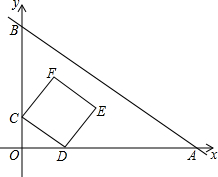 如图,在平面直角坐标系中,直线AB经过点A(4,0),B(0,3),动点C从点O出发,以每秒3个单位长度的速度向点B运动,过点C作CD∥AB于OA于点D,以CD为边向上作正方形CDEF,设正方形CDEF与△AOB重合部分图形的面积为y,运动时间为t.
如图,在平面直角坐标系中,直线AB经过点A(4,0),B(0,3),动点C从点O出发,以每秒3个单位长度的速度向点B运动,过点C作CD∥AB于OA于点D,以CD为边向上作正方形CDEF,设正方形CDEF与△AOB重合部分图形的面积为y,运动时间为t.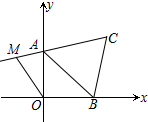 如图所示,在平面直角坐标系中,A(0,3)、B(3,0)、C(4,4),线段CA的延长线上有一点M,使四边形ABOM的面积与三角形ABC的面积相等,则M的坐标为(-2,$\frac{5}{2}$).
如图所示,在平面直角坐标系中,A(0,3)、B(3,0)、C(4,4),线段CA的延长线上有一点M,使四边形ABOM的面积与三角形ABC的面积相等,则M的坐标为(-2,$\frac{5}{2}$). 如图,点C是以AB为直径的半圆上一点,∠ACB=90°,AC=3,BC=4,则图中阴影部分的面积是$\frac{25π}{8}$-6.
如图,点C是以AB为直径的半圆上一点,∠ACB=90°,AC=3,BC=4,则图中阴影部分的面积是$\frac{25π}{8}$-6.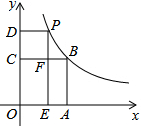 如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,边OA在x轴正半轴上,点B、P都在函数y=$\frac{4}{x}$(x>0)的图象上,过点P分别作x轴、y轴的平行线,交于点D、E.点P在点B的上方.若CD:CO=1:2,矩形OEFC的面积是$\frac{8}{3}$.
如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,边OA在x轴正半轴上,点B、P都在函数y=$\frac{4}{x}$(x>0)的图象上,过点P分别作x轴、y轴的平行线,交于点D、E.点P在点B的上方.若CD:CO=1:2,矩形OEFC的面积是$\frac{8}{3}$.