题目内容
计算
(1)先化简,再求值:(2x﹣1)(x+2)﹣2x(x+1),x=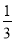 .
.
(2)已知:a+b=4,ab=3,求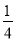 a3b+
a3b+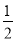 a2b2+
a2b2+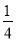 ab3的值.
ab3的值.
因式分【解析】
(1)(a+b)2+6(a+b)+9; (2)(x﹣y)2﹣9(x+y)2;
(3)a2(x﹣y)+b2(y﹣x). (4)(x2-5)2+8(5-x2)+16.
查看答案计算
(1)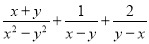 (2)
(2)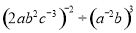
(3)a5·a7+a6·(-a3)2+2(-a3)4; (4)(x+2y﹣z)(x﹣2y+z)
查看答案已知关于x的分式方程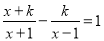 的解为负数,则k的取值范围是_________
的解为负数,则k的取值范围是_________
若x、y满足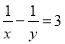 ,则分式
,则分式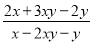 的值为_________.
的值为_________.
生物学家发现一种病毒的长度约为0.000 043毫米,用科学记数法表示为_____米.
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案在下列“禁毒”“和平”“志愿者”“节水”这四个标志中,属于轴对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
从2012年4月1日起厦门市实行新的自来水收费阶梯水价,收费标准如下表所示:
月用水量 | 不超过15吨的部分 | 超过15吨不超过25吨的部分 | 超过25吨的部分 |
收费标准 (元/吨) | 2.2 | 3.3 | 4.4 |
备注:①.每月居民用水缴费包括实际用水的水费和污水处理费两部分.
②.以上表中的价格均不包括1元/吨的污水处理费
(1)某用户12月份用水量为20吨,则该用户12月份应缴水费是多少?
(2)若某用户的月用水量为m吨,请用含m的式子表示该用户月所缴水费.
查看答案小明乘公共汽车到东方明珠玩,小明上车时,发现车上已有(6a﹣2b)人,车到中途时,有一半人下车,但又上来若干人,这时公共汽车上共有(10a﹣6b)人,则中途上车多少人?当a=5,b=3时,中途上车的人数.
查看答案定义:若a+b=2,则称a与b是关于1的平衡数.
(1)3与 是关于1的平衡数,5﹣x与 是关于1的平衡数.(用含x的代数式表示)
(2)若a=2x2﹣3(x2+x)+4,b=2x﹣[3x﹣(4x+x2)﹣2],判断a与b是否是关于1 的平衡数,并说明理由.
查看答案某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):

(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)本周总的生产量是多少辆?
查看答案某一出租车一天下午以鼓楼为出发地在东西方向营运,向东走为正,向西走为负,行车里程(单位:千米)依先后次序记录如下:+9,﹣3,﹣5,+4,﹣10,+6,﹣3,﹣6,﹣4,+10
(1)将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼的什么方向?
(2)若出租车每千米的耗油量为0.08升,这天下午出租车共耗油量多少升?
查看答案 试题属性- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图1,已知正方形ABCD的边长为1,点E在边BC上,若∠AEF=90°,且EF交正方形的外角∠DCM的平分线CF于点F.

(1)图1中若点E是边BC的中点,我们可以构造两个三角形全等来证明AE=EF,请叙述你的一个构造方案,并指出是哪两个三角形全等(不要求证明);
(2)如图2,若点E在线段BC上滑动(不与点B,C重合).
①AE=EF是否一定成立?说出你的理由;
②在如图2所示的直角坐标系中抛物线y=ax2+x+c经过A、D两点,当点E滑动到某处时,点F恰好落在此抛物线上,求此时点F的坐标.
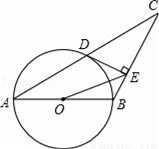
(1)见解析;(2)①见解析;②点F的坐标为F(,) 【解析】试题分析:(1)由于∠AEF=90°,故∠FEC=∠EAB,而E是BC中点,从而只需取AB点G,连接EG,则有AG=CE,BG=BE,∠AGE=∠ECF,易得△AGE≌△ECF; (2)①由于AB=BC,所以只要AG=EC就有BG=BE,就同样可得△AGE≌△ECF,于是截取AG=EC,证全等即可; ②根据A、D两点的...如图,已知△ABC中,AB=BC,以AB为直径的圆O交AC于点D,过点D作DE⊥BC,垂足为E,连接OE.
(1)求证:DE是⊙O的切线;
(2)若CD=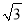 ,∠ACB=30°,求OE的长.
,∠ACB=30°,求OE的长.
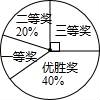
国务院办公厅在2015年3月16日发布了《中国足球发展改革总体方案》,这是中国足球史上的重大改革,为进一步普及足球知识,传播足球文化,我市某区在中小学举行了“足球在身边”知识竞赛,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题:
(1)获得一等奖的学生人数;
(2)在本次知识竞赛活动中,A,B,C,D四所学校表现突出,现决定从这四所学校中随机选取两所学校举行一场足球友谊赛,请用画树状图或列表的方法求恰好选到A,B两所学校的概率.
某基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长54米的不锈钢栅栏围成,与墙平行的一边留一个宽为2米的出入口,如图所示,如何设计才能使园地的而积最大?下面是两位学生争议的情境:请根据上面的信息,解决问题:

(1)设AB=x米(x>0),试用含x的代数式表示BC的长;
(2)请你判断谁的说法正确,为什么?
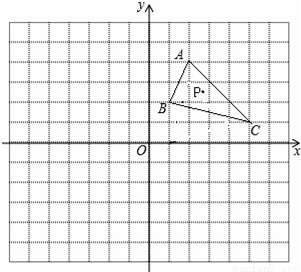
查看答案在如图所示平面直角坐标系中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上.
(1)以O为旋转中心,将△ABC逆时针旋转90°,画出旋转后的△A1B1C1;
(2)画出△A1B1C1关于原点对称的△A2B2C2;
(3)若△ABC内有一点P(a,b),结果上面两次变换后点P在△A2B2C2中的对应点为P′,则点P′的坐标为 .
现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,长沙市某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率;
(2)如果平均每人每月最多可投递0.6万件,那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务?
查看答案 试题属性- 题型:解答题
- 难度:困难
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
下列成语中,属于随机事件的是( )
A. 水中捞月 B. 瓮中捉鳖 C. 守株待兔 D. 探囊取物
C 【解析】试题分析:A.水中捞月是不可能事件,故A错误; B.瓮中捉鳖是必然事件,故B错误; C.守株待兔是随机事件,故C正确; D.探囊取物是必然事件,故D错误; 故选C. 考点:随机事件.下列命题中,不正确的是( )
A. 垂直平分弦的直线经过圆心 B. 平分弦的直径一定垂直于弦
C. 平行弦所夹的两条弧相等  D. 垂直于弦的直径必平分弦所对的弧
D. 垂直于弦的直径必平分弦所对的弧
二次函数y=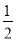 (x﹣1)2+2的图象可由y=
(x﹣1)2+2的图象可由y=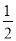 x2的图象( )
x2的图象( )
A. 向左平移1个单位,再向下平移2个单位得到
B. 向左平移1个单位,再向上平移2个单位得到
C. 向右平移1个单位,再向下平移2个单位得到
D. 向右平移1个单位,再向上平移2个单位得到
查看答案如图,将正方形图案绕中心O旋转180°后,得到的图案是( )
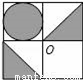
A.  B.
B.  C.
C. 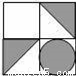 D.
D. 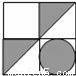
下列方程是关于x的一元二次方程的是( )
A. ax2+bx+c=0 B. 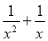 =2 C. x2+2x=x2﹣1 D. 3(x+1)2=2(x+1)
=2 C. x2+2x=x2﹣1 D. 3(x+1)2=2(x+1)
阅读材料:若m2﹣2mn+2n2﹣8n+16=0,求m、n的值.
【解析】
∵m2﹣2mn+2n2﹣8n+16=0,∴(m2﹣2mn+n2)+(n2﹣8n+16)=0
∴(m﹣n)2+(n﹣4)2=0,∴(m﹣n)2=0,(n﹣4)2=0,∴n=4,m=4.
根据你的观察,探究下面的问题:
(1)已知x2﹣2xy+2y2+6y+9=0,求xy的值;
(2)已知△ABC的三边长a、b、c都是正整数,且满足a2+b2﹣10a﹣12b+61=0,求△ABC的最大边c的值;
(3)已知a﹣b=8,ab+c2﹣16c+80=0,求a+b+c的值.
查看答案 试题属性- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
若x=2m+1,y=3+4m.
(1)请用含x的代数式表示y;
(2)如果x=4,求此时y的值.
(1) y=x2﹣2x+4;(2)12. 【解析】试题分析:(1)将4m变形,转化为关于2m的形式,然后再代入整理即可; (2)把x=4代入解得即可. 试题解析:(1)∵4m=22m=(2m)2,x=2m+1, ∴2m=x﹣1, ∵y=4m+3, ∴y=(x﹣1)2+3, 即y=x2﹣2x+4; (2)把x=4代入y=x2﹣2x+4=12.解答一个问题后,将结论作为条件之一,提出与原问题有关的新问题,我们把它称为原问题的一个“逆向”问题.例如,原问题是“若矩形的两边长分别为3和4,求矩形的周长”,求出周长等于14后,它的一个“逆向”问题可以是“若矩形的周长为14,且一边长为3,求另一边的长”;也可以是“若矩形的周长为14,求矩形面积的最大值”,等等.
(1)设A=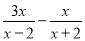 ,B=
,B=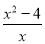 ,求A与B的积;
,求A与B的积;
(2)提出(1)的一个“逆向”问题,并解答这个问题.
查看答案按要求完成下列各题:
(1)已知实数a、b满足(a+b)2=1,(a﹣b)2=9,求a2+b2﹣ab的值;
(2)已知(2015﹣a)(2016﹣a)=2047,试求(a﹣2015)2+(2016﹣a)2的值.
查看答案请先将下式化简,再选择一个适当的数代入求值.(1﹣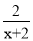 )﹣
)﹣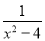 ÷
÷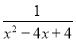 .
.
解方程
(1)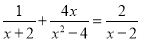 (2)
(2)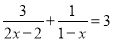
计算
(1)先化简,再求值:(2x﹣1)(x+2)﹣2x(x+1),x=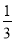 .
.
(2)已知:a+b=4,ab=3,求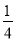 a3b+
a3b+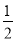 a2b2+
a2b2+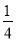 ab3的值.
ab3的值.
- 题型:解答题
- 难度:困难
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
生物学家发现一种病毒的长度约为0.000 043毫米,用科学记数法表示为_____米.
【解析】试题解析:绝对值<1的正数也可以利用科学记数法表示,一般形式为a×10-n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定. 故0.000043mm=4.3×10-5mm. 点睛:用科学记数法表示较小的数,一般形式为a×10-n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数.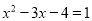 ,
, 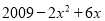 = _______
= _______
汽车从甲地开往乙地,每小时行驶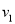 千米,t小时可到达.如果每小时多行驶
千米,t小时可到达.如果每小时多行驶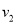 千米,那么可以提前_______小时到达。
千米,那么可以提前_______小时到达。
分式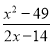 约分的结果是_______
约分的结果是_______
若x2+mxy+16y2是完全平方式,则m= ________
查看答案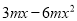 中公因式是___________
中公因式是___________
- 题型:填空题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
计算(x2-3x+n)(x2+mx+8)的结果中不含x2和x3的项,则m,n的值为( )
A. m=3,n=1 B. m=0,n=0 C. m=-3,n=-9 D. m=-3,n=8
A 【解析】试题解析:(x2-3x+n)(x2+mx+8) =x4+mx3+8x2-3x3-3mx2-24x+nx2+nmx+8n =x4+(m-3)x3+(8-3m+n)x2-24x+8n, ∵不含x2和x3的项, ∴m-3=0, ∴m=3. ∴8-3m+n=0, ∴n=1. 故选A.若关于x的分式方程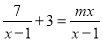 无解,则实数m的值是( )
无解,则实数m的值是( )
A. x=0或1 B. x=1或3 C. x=3或7 D. x=0或3
查看答案某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需时间与原计划生产450台机器所需时间相同.设原计划平均每天生产x台机器,根据题意,下面所列方程正确的是( )
A. 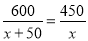 B.
B. 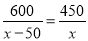 C.
C. 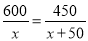 D.
D. 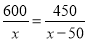
能使分式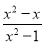 的值为零的所有x的值是( )
的值为零的所有x的值是( )
A. x=1 B. x=0 C. x=0或x=1 D. x=0或x=±1
查看答案若把分式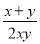 中的x和y都扩大3倍,那么分式的值( )
中的x和y都扩大3倍,那么分式的值( )
A. 扩大3倍 B. 不变 C. 缩小3倍 D. 缩小6倍
查看答案与分式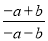 相等的是( )
相等的是( )
A. 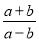 B.
B. 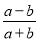 C.
C. 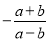 D.
D. 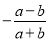
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
解一元二次方程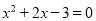
如图,在三角形ABC中,AB=24,AC=18,D是AC上一点,AD=12,在AB上取一点E,使A、D、E三点组成的三角形与ABC相似,则AE=__________.

函数 是
是 关于
关于 的反比例函数,则
的反比例函数,则 _______.
_______.
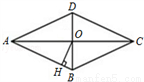
如图,菱形ABCD的对角线AC、BD相交于点O,且AC=8,BD=6,过点O作OH丄AB,垂足为H,则点0到边AB的距离OH=_____.
一个直角三角形斜边上的高与中线分别是5㎝和6㎝,则它的面积是______ 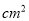 .
.
反比例函数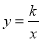 经过点(-2,1),则一次函数
经过点(-2,1),则一次函数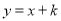 的图象经过点(-1,_____).
的图象经过点(-1,_____).
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
已知反比例函数 ,下列结论不正确的是
,下列结论不正确的是
A.图象必经过点(-1,2) B.y随x的增大而增大
C.图象在第二、四象限内D.若x>1,则y>-2
B 【解析】 试题分析:点(-1,2)满足反比例函数,所以图象必经过点(-1,2);-2<0,在各自区间内, y随x的增大而增大,图象在第二、四象限内,所以B错误;在第四象限,y随x的增大而增大,x>1,则y>-2 考点:反比例函数在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以每秒1cm的速度移动,同时点Q从点B出发沿BC边向点C以每秒2cm的速度移动P、Q两点在分别到达B、C两点后就停止移动,设两点移动的时间为t秒,回答下列问题:
(1)如图1,当t为几秒时,△PBQ的面积等于5cm2?
(2)如图2,当t= 秒时,试判断△DPQ的形状,并说明理由;
秒时,试判断△DPQ的形状,并说明理由;
(3)如图3,以Q为圆心,PQ为半径作⊙Q.
①在运动过程中,是否存在这样的t值,使⊙Q正好与四边形DPQC的一边(或边所在的直线)相切?若存在,求出t值;若不存在,请说明理由;
②若⊙Q与四边形DPQC有三个公共点,请直接写出t的取值范围.

已知A、B、C、D是⊙O上的四点, 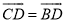 ,AC是四边形ABCD的对角线
,AC是四边形ABCD的对角线
(1)如图1,连结BD,若∠CDB=60°,求证:AC是∠DAB的平分线;
(2)如图2,过点D作DE⊥AC,垂足为E,若AC=7,AB=5,求线段AE的长度.

小丽为校合唱队购买某种服装时,商店经理给出了如下优惠条件:如果一次性购买不超过10件,单价为80元;如果一次性购买多于10件,那么每增加1件,购买的所有服装的单价降低2元,但单价不得低于50元.按此优惠条件,小丽一次性购买这种服装付了1200元.请问她购买了多少件这种服装?
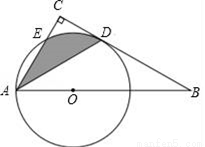
查看答案如图,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与边BC交于点D,与边AC交于点E,连接AD,且AD平分∠BAC.
(1)试判断BC与⊙O的位置关系,并说明理由;
(2)若∠BAC=60°,OA=2,求阴影部分的面积(结果保留π).
受益于国家支持新能源汽车发展和“一带一路”发展战略等多重利好因素,我市某汽车零部件生产企业的利润逐年提高,据统计,2014年利润为2亿元,2016年利润为2.88亿元.
(1)求该企业从2014年到2016年利润的年平均增长率;
(2)若2017年保持前两年利润的年平均增长率不变,该企业2017年的利润能否超过3.4亿元?
查看答案 试题属性- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧

