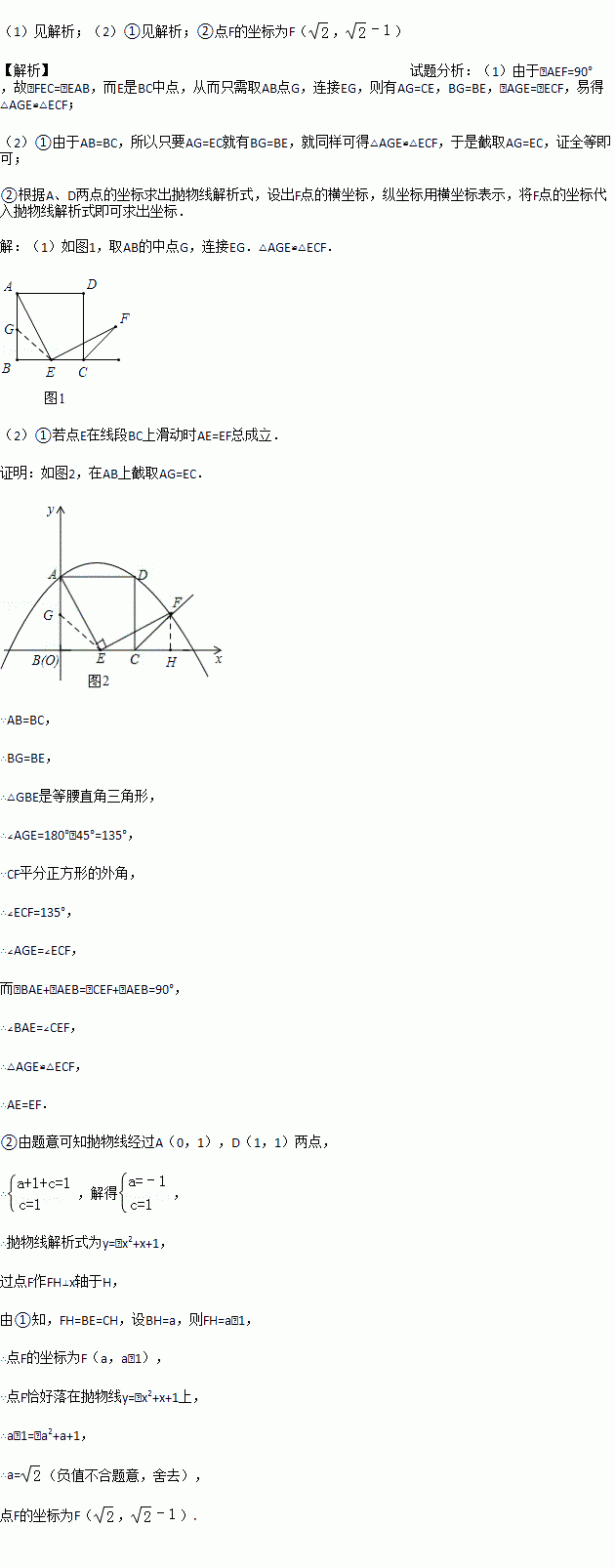题目内容
如图1,已知正方形ABCD的边长为1,点E在边BC上,若∠AEF=90°,且EF交正方形的外角∠DCM的平分线CF于点F.

(1)图1中若点E是边BC的中点,我们可以构造两个三角形全等来证明AE=EF,请叙述你的一个构造方案,并指出是哪两个三角形全等(不要求证明);
(2)如图2,若点E在线段BC上滑动(不与点B,C重合).
①AE=EF是否一定成立?说出你的理由;
②在如图2所示的直角坐标系中抛物线y=ax2+x+c经过A、D两点,当点E滑动到某处时,点F恰好落在此抛物线上,求此时点F的坐标.
(1)见解析;(2)①见解析;②点F的坐标为F(,) 【解析】试题分析:(1)由于∠AEF=90°,故∠FEC=∠EAB,而E是BC中点,从而只需取AB点G,连接EG,则有AG=CE,BG=BE,∠AGE=∠ECF,易得△AGE≌△ECF; (2)①由于AB=BC,所以只要AG=EC就有BG=BE,就同样可得△AGE≌△ECF,于是截取AG=EC,证全等即可; ②根据A、D两点的...如图,已知△ABC中,AB=BC,以AB为直径的圆O交AC于点D,过点D作DE⊥BC,垂足为E,连接OE.
(1)求证:DE是⊙O的切线;
(2)若CD=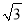 ,∠ACB=30°,求OE的长.
,∠ACB=30°,求OE的长.
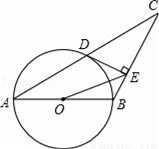
国务院办公厅在2015年3月16日发布了《中国足球发展改革总体方案》,这是中国足球史上的重大改革,为进一步普及足球知识,传播足球文化,我市某区在中小学举行了“足球在身边”知识竞赛,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题:
(1)获得一等奖的学生人数;
(2)在本次知识竞赛活动中,A,B,C,D四所学校表现突出,现决定从这四所学校中随机选取两所学校举行一场足球友谊赛,请用画树状图或列表的方法求恰好选到A,B两所学校的概率.
某基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长54米的不锈钢栅栏围成,与墙平行的一边留一个宽为2米的出入口,如图所示,如何设计才能使园地的而积最大?下面是两位学生争议的情境:请根据上面的信息,解决问题:

(1)设AB=x米(x>0),试用含x的代数式表示BC的长;
(2)请你判断谁的说法正确,为什么?
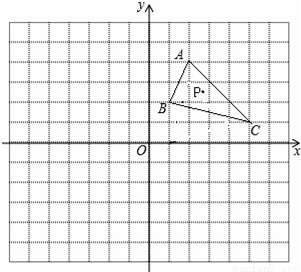
查看答案在如图所示平面直角坐标系中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上.
(1)以O为旋转中心,将△ABC逆时针旋转90°,画出旋转后的△A1B1C1;
(2)画出△A1B1C1关于原点对称的△A2B2C2;
(3)若△ABC内有一点P(a,b),结果上面两次变换后点P在△A2B2C2中的对应点为P′,则点P′的坐标为 .
现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,长沙市某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率;
(2)如果平均每人每月最多可投递0.6万件,那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务?
查看答案 试题属性- 题型:解答题
- 难度:困难
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
 阅读快车系列答案
阅读快车系列答案今年某县有1万名初中和小学生参加全国义务教育质量抽测,为了了解1万名学生的抽测成绩,从中抽取500名学生抽测成绩进行统计分析,在这个问题中数据500是( )
A. 总体 B. 个体 C. 一个样本 D. 样本容量
D 【解析】【解析】 为了了解1万名学生的抽测成绩,从中抽取500名学生抽测成绩进行统计分析,在这个问题中数据500是样本容量,故选D. 点睛:考查了总体、个体、样本、样本容量.解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.下面调查方式中,合适的是( )
A. 调查你所在班级同学的身高,采用抽样调查方式
B. 调查湘江的水质情况,采用抽样调查的方式
C. 调查CCTV﹣5《NBA 总决赛》栏目在我市的收视率,采用普查的方式
D. 要了解全市初中学生的业余爱好,采用普查的方式
查看答案光年是天文学中的距离单位,1光年大约是9500 000 000 000 km,用科学记数法可表示为( )
A、950×1010 km B、95×1011 km C、9.5×1012 km D、0.95×1013 km
查看答案如图示,数轴上点A所表示的数的绝对值为( )
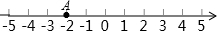
A.2 B.﹣2 C.±2 D.以上均不对
查看答案在数﹣(﹣3),0,(﹣3)2,|﹣9|,﹣14中,正数的有( )个.
A. 2 B. 3 C. 4 D. 5
查看答案﹣ 的相反数是( )
的相反数是( )
A. ﹣5 B. 5 C. ﹣ D.
D. 
- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
定义新运算符号“⊕”如下:a⊕b=a﹣b﹣1,则2⊕(﹣3)=_____.
4 【解析】根据题中的新定义得:2⊕(﹣3)=2﹣(﹣3)﹣1=2+3﹣1=4, 故答案为:4a,b互为相反数,c,d互为倒数,则(a+b)3﹣3(cd)4=_____.
查看答案已知|a+3|+(b-1)2=0,则3a+b=__________.
查看答案单项式-2x2y的次数是 .
查看答案根治水土流失刻不容缓,目前全国水土流失面积已达36700000米2,用科学记数法表示为______米2.
查看答案﹣2的绝对值是_____.
查看答案 试题属性- 题型:填空题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
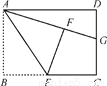
如图,E是矩形ABCD中BC边的中点,将△ABE沿AE折叠到△AEF,F在矩形ABCD内部,延长AF交DC于G点,若∠AEB=55°,∠DAF=________.
反比例函数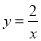 中自变量x的取值范围是________。
中自变量x的取值范围是________。
如图,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC=( )
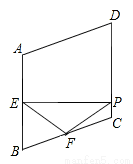
A. 35° B. 45° C. 50° D. 55°
查看答案若α是锐角,sinαcosα=p,则sinα+cosα的值是( )
A. 1+2p B. 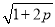 C. 1-2p D.
C. 1-2p D. 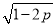
函数y=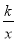 与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
A. 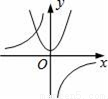 B.
B. 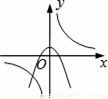 C.
C. 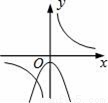 D.
D. 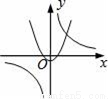
走入考场之前老师送你一句话“Wish you success”。在这句话中任选一个字母,这个字母为“s”的概率是( )
A. 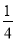 B.
B. 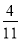 C.
C. 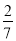 D.
D. 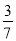
- 题型:填空题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
一根笔直的小木棒(记为线段AB),它的正投影为线段CD,则下列各式中,一定成立的是( )
A. AB=CD B. AB≤CD C. AB≥CD D. AB>CD
C 【解析】试题解析:根据正投影的定义,当AB与投影面平行时,AB=CD,当AB与投影面不平行时,AB大于CD.故选C. 点睛:投影线垂直于投影底幕面时,称正投影. 同一物体的所处的位置不同得到正投影也不同.若反比例函数y=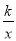 的图象经过点(m,3m),其中m≠0,则反比例函数的图象在( )
的图象经过点(m,3m),其中m≠0,则反比例函数的图象在( )
A. 第一、二象限 B. 第一、三象限 C. 第二、四象限 D. 一、三或二、四象限
查看答案在△ABC中,若tanA=1,sinB=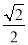 ,你认为最确切的判断是( )
,你认为最确切的判断是( )
A. △ABC是等腰三角形 B. △ABC是等腰直角三角形
C. △ABC是直角三角形 D. △ABC是一般锐角三角形
查看答案下列函数中,不是二次函数( )
A. 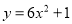 B.
B. 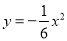 C.
C. 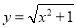 D.
D. 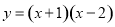
用配方法解一元二次方程x²-4x-5=0,此方程可变形为( )
A. (x-2)²=9 B. (x+2)²=9 C. (x+2)²=1 D. (x-2)²=1
查看答案如图1,已知正方形ABCD的边长为1,点E在边BC上,若∠AEF=90°,且EF交正方形的外角∠DCM的平分线CF于点F.

(1)图1中若点E是边BC的中点,我们可以构造两个三角形全等来证明AE=EF,请叙述你的一个构造方案,并指出是哪两个三角形全等(不要求证明);
(2)如图2,若点E在线段BC上滑动(不与点B,C重合).
①AE=EF是否一定成立?说出你的理由;
②在如图2所示的直角坐标系中抛物线y=ax2+x+c经过A、D两点,当点E滑动到某处时,点F恰好落在此抛物线上,求此时点F的坐标.
查看答案 试题属性- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,长沙市某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率;
(2)如果平均每人每月最多可投递0.6万件,那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务?
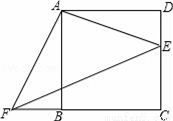
(1)10%;(2)不能. 【解析】试题分析:(1)利用增长率列一元二次方程.(2)由增长率公式计算,比较大小. 试题解析: (1)设该快递公司投递总件数的月平均增长率为x,根据题意得 10(1+x)2=12.1, 解得x1=0.1,x2=﹣2.1(不合题意舍去). 答:该快递公司投递总件数的月平均增长率为10%; (2)今年6月份的快递投递任务是12.1...四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.
(1)求证:△ADE≌△ABF;
(2)若BC=8,DE=6,求△AEF的面积.
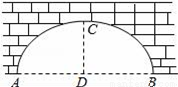
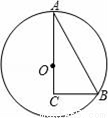
如图,圆弧形桥拱的跨度AB=12米,拱高CD=4米,求拱桥的半径.
如图,Rt△ABC中,∠C=90°、∠A=30°,在AC边上取点O画圆,使⊙O经过A、B两点,下列结论正确的序号是____________
①AO=2CO;②AO=BC;③以O为圆心,以OC为半径的圆与AB相切;④延长BC交⊙O与D,则A、B、D是⊙O的三等分点.
在同一平面上一点P到⊙O的距离最长为7cm,最短为3m,则⊙O的半径为____cm.
查看答案己知拋物线y=x2﹣2x﹣3,当﹣2≤x≤0时,y的取值范围是____________
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:
①abc<0;
②2a﹣b=0;
③4a+2b+c<0;
④若(﹣5,y1),(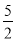 ,y2)是抛物线上两点,则y1>y2.
,y2)是抛物线上两点,则y1>y2.
其中说法正确的是( )
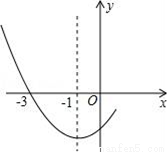
A. ①② B. ②③ C. ①②④ D. ②③④
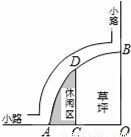
C 【解析】试题解析:①抛物线开口向上,a>0,物线与y轴交于负半轴,c<0,-=-1,b>0,∴abc<0,①正确; ②-=-1,2a-b=0,②正确; ③x=2时,y>0,4a+2b+c>0,③不正确; ④∵对称轴是直线x=-1,所以x=-5和x=3时,y值相等,∴y1>y2,④正确 故选C.如图是某公园的一角,∠AOB=90°,弧AB的半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是( )
A. (10π﹣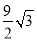 )米2 B. (π﹣
)米2 B. (π﹣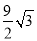 )米2 C. (6π﹣
)米2 C. (6π﹣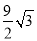 )米2 D. (6π﹣
)米2 D. (6π﹣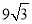 )米2
)米2
现有一张圆心角为108°,半径为40cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为10cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的圆心角θ为 度
A. 18 B. 30 C. 45 D . 60
查看答案在如图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心可能是( )
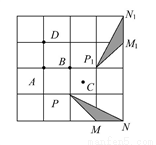
A. 点A B. 点B C. 点C D. 点D
查看答案在一个不透明的盒子中有20个除颜色外均相同的小球,每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复摸球试验后,发现摸到红球的频率稳定于0.3,由此可估计盒中红球的个数约为( )
A. 3 B. 6 C. 7 D. 14
查看答案下列成语中,属于随机事件的是( )
A. 水中捞月 B. 瓮中捉鳖 C. 守株待兔 D. 探囊取物
查看答案 试题属性- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
计算
(1)先化简,再求值:(2x﹣1)(x+2)﹣2x(x+1),x=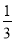 .
.
(2)已知:a+b=4,ab=3,求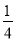 a3b+
a3b+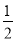 a2b2+
a2b2+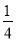 ab3的值.
ab3的值.
因式分【解析】
(1)(a+b)2+6(a+b)+9; (2)(x﹣y)2﹣9(x+y)2;
(3)a2(x﹣y)+b2(y﹣x). (4)(x2-5)2+8(5-x2)+16.
查看答案计算
(1)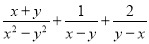 (2)
(2)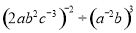
(3)a5·a7+a6·(-a3)2+2(-a3)4; (4)(x+2y﹣z)(x﹣2y+z)
查看答案已知关于x的分式方程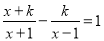 的解为负数,则k的取值范围是_________
的解为负数,则k的取值范围是_________
若x、y满足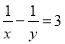 ,则分式
,则分式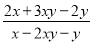 的值为_________.
的值为_________.
生物学家发现一种病毒的长度约为0.000 043毫米,用科学记数法表示为_____米.
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图是同一时刻学校里一棵树和旗杆的影子,如果树高为3米,测得它的影子长为1.2米,旗杆的高度为5米,则它的影子长为( )
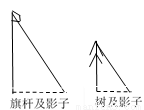
A. 4米 B. 2米 C. 1.8米 D. 3.6米
B 【解析】设旗杆的影子长x,由题意知两个图形相似,所以,解得x=2米,所以选B.关于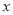 的一元二次方程
的一元二次方程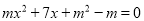 的常数项为0,则
的常数项为0,则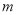 的值等于( )
的值等于( )
A. 1 B. 2 C. 0或1 D. 0
查看答案下列各组线段(单位:cm)中,成比例线段的是 ( )
A. 1、2、3、4 B. 1、2、2、4 C. 3、5、9、13 D. 1、2、2、3
查看答案准备两组相同的牌,每组两张且大小相同,两张牌的牌面数字分别是0,1,从每组牌中各摸出一张牌,两张牌的牌面数字和为1的概率为( )
A. 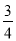 B.
B. 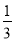 C.
C. 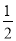 D.
D. 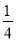
点P(-2, 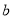 )是反比例函数
)是反比例函数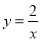 的图象上的一点,则
的图象上的一点,则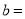 ( )
( )
A. 2 B. 1 C. -2 D. -1
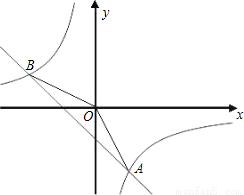
查看答案已知一次函数y= kx+b的图象与反比例函数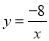 的图象相交于A,B两点, 其中A点的横坐标与B点的纵坐标都是2,如图:
的图象相交于A,B两点, 其中A点的横坐标与B点的纵坐标都是2,如图:
(1)求这个一次函数的解析式;
(2)在y轴是否存在一点P使△OAP为等腰三角形?若存在,请求出符合条件的点P坐标;若不存在,请说明理由.
- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧