题目内容
若一个正多边形的边心距与边长之比为
,则此正多边形是( )
| ||
| 2 |
| A、正十二边形 | B、正三角形 |
| C、正六边形 | D、正方形 |
考点:正多边形和圆
专题:
分析:根据题意画出图形,设正多边形的边长为2a,则其边心距为
a,故可得出其底角的度数,由此可判断出△OAB的形状,故可得出结论.
| 3 |
解答: 解:如图所示:
解:如图所示:
∵正多边形的边心距与边长之比为
,
∴设正多边形的边长为2a,则其边心距为
a,
∵OD⊥AB,
∴AD=
AB=
×2a=a,
∴tan∠OAD=
=
=
,
∴∠OAB=60°,
∵OA=OB,
∴△OAB是等边三角形,
∴∠AOB=60°,
∴n=
=6.
∴此正多边形是正六边形.
故选C.
 解:如图所示:
解:如图所示:∵正多边形的边心距与边长之比为
| ||
| 2 |
∴设正多边形的边长为2a,则其边心距为
| 3 |
∵OD⊥AB,
∴AD=
| 1 |
| 2 |
| 1 |
| 2 |
∴tan∠OAD=
| OD |
| AD |
| ||
| a |
| 3 |
∴∠OAB=60°,
∵OA=OB,
∴△OAB是等边三角形,
∴∠AOB=60°,
∴n=
| 360 |
| 60 |
∴此正多边形是正六边形.
故选C.
点评:本题考查的是正多边形和圆,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
相关题目
下列运算中正确的是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
 如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=2,BC=3,将DC绕点D逆时针旋转90°得到点E,求△ADE的面积.
如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=2,BC=3,将DC绕点D逆时针旋转90°得到点E,求△ADE的面积. 如图,直线y=x+b(b≠0)交坐标轴于A、B两点,交双曲线y=
如图,直线y=x+b(b≠0)交坐标轴于A、B两点,交双曲线y=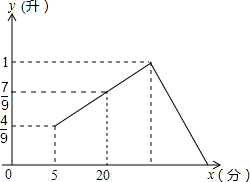 有一个附有进、出水管的水池,每单位时间的进、出水量一定.设从某一时刻开始只进水,5分钟后水池的蓄水量恰好占全池的
有一个附有进、出水管的水池,每单位时间的进、出水量一定.设从某一时刻开始只进水,5分钟后水池的蓄水量恰好占全池的 函数y=3-|x-2|的图象如图所示,则点B的坐标是
函数y=3-|x-2|的图象如图所示,则点B的坐标是 如图,AB是⊙O的直径,AC是⊙O的弦,以OA为直径的⊙D与AC相交于点E.
如图,AB是⊙O的直径,AC是⊙O的弦,以OA为直径的⊙D与AC相交于点E.