题目内容
4.先化简,再求值:[$\frac{{x}^{2}-1}{{(x-1)}^{2}}$-$\frac{x}{x-1}$]÷$\frac{1}{x}$,其中x=tan45°-6sin30°.分析 原式括号中第一项约分后,利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解答 解:原式=[$\frac{(x+1)(x-1)}{(x-1)^{2}}$-$\frac{x}{x-1}$]•x=$\frac{1}{x-1}$•x=$\frac{x}{x-1}$,
当x=tan45°-6sin30°=1-3=-2时,原式=$\frac{2}{3}$.
点评 此题考查了分式的化简求值,以及特殊角的三角函数值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
12. 如图,正方形ABCD中,AB=4,点E是边BC的中点,点G,H分别是边CD,AB上的动点,连接GH交AE于F,且使GH⊥AE,连接AG,EH,则EH+AG的最小值是( )
如图,正方形ABCD中,AB=4,点E是边BC的中点,点G,H分别是边CD,AB上的动点,连接GH交AE于F,且使GH⊥AE,连接AG,EH,则EH+AG的最小值是( )
 如图,正方形ABCD中,AB=4,点E是边BC的中点,点G,H分别是边CD,AB上的动点,连接GH交AE于F,且使GH⊥AE,连接AG,EH,则EH+AG的最小值是( )
如图,正方形ABCD中,AB=4,点E是边BC的中点,点G,H分别是边CD,AB上的动点,连接GH交AE于F,且使GH⊥AE,连接AG,EH,则EH+AG的最小值是( )| A. | 8 | B. | 4$\sqrt{5}$ | C. | 2$\sqrt{10}$ | D. | 8$\sqrt{2}$ |
19.十一黄金周时期,某旅游区的游客知表:
(1)求这7天假期中,游客量的平均数、中位数和众数;
(2)选用平均数、中位数和众数中的哪个数作代表,更能反映黄金周7天游客量的一般情况?
| 人数/万人 | 0.6 | 1.2 | 2 | 2.5 |
| 天数 | 2 | 1 | 3 | 1 |
(2)选用平均数、中位数和众数中的哪个数作代表,更能反映黄金周7天游客量的一般情况?
9.若把一次函数y=2x-3,向下平移3个单位长度,得到图象解析式是( )
| A. | y=2x | B. | y=2x-6 | C. | y=5x-3 | D. | y=-x-3 |
13.4的平方根是( )
| A. | -2 | B. | 2 | C. | ±2 | D. | 16 |
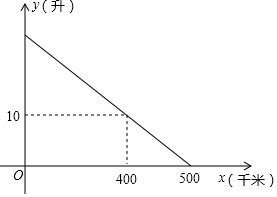 已知某汽车装满油后邮箱中的剩余油量y(升)与汽车的行驶路程x(千米)之间具有一次函数关系(如图所示),为了行驶安全考虑,邮箱中剩余油量不能低于5升,那么这辆汽车装满油后至多行驶450千米,就应该停车加油.
已知某汽车装满油后邮箱中的剩余油量y(升)与汽车的行驶路程x(千米)之间具有一次函数关系(如图所示),为了行驶安全考虑,邮箱中剩余油量不能低于5升,那么这辆汽车装满油后至多行驶450千米,就应该停车加油.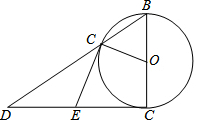 如图,⊙O的直径AB=4,点C为⊙O上的一个动点,连接OC,过点A作⊙O的切线,与BC的延长线交于点D,点E为AD的中点,连接CE.
如图,⊙O的直径AB=4,点C为⊙O上的一个动点,连接OC,过点A作⊙O的切线,与BC的延长线交于点D,点E为AD的中点,连接CE.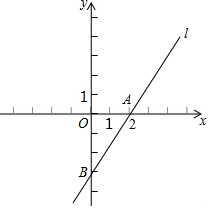 如图,在平面直角坐标系xOy中,过点A(2,0)的直线l:y=mx-3与y轴交于点B.
如图,在平面直角坐标系xOy中,过点A(2,0)的直线l:y=mx-3与y轴交于点B.