题目内容
16.已知一个菱形的边长为5,其中一条对角线长为8,则这个菱形的面积为24.分析 首先根据题意画出图形,由一个菱形的边长为5,其中一条对角线长为8,可利用勾股定理,求得另一菱形的长,继而求得答案.
解答  解:如图,∵菱形ABCD中,BD=8,AB=5,
解:如图,∵菱形ABCD中,BD=8,AB=5,
∴AC⊥BD,OB=$\frac{1}{2}$BD=4,
∴OA=$\sqrt{A{B}^{2}-O{B}^{2}}$=3,
∴AC=2OA=6,
∴这个菱形的面积为:$\frac{1}{2}$AC•BD=$\frac{1}{2}$×6×8=24.
故答案为:24.
点评 此题考查了菱形的性质以及勾股定理.注意菱形的面积等于其对角线积的一半.

练习册系列答案
相关题目
4.直角三角形的两锐角平分线相交成的角的度数是( )
| A. | 45° | B. | 135° | C. | 45°或135° | D. | 以上答案均不对 |
8.直线y=2x-3与直线y=kx+1平行,则k等于( )
| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
5.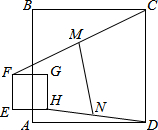 如图,边长为2的正方形EFGH在边长为6的正方形ABCD所在平面上移动,始终保持EF∥AB.线段CF的中点为M,DH的中点为N,则线段MN的长为( )
如图,边长为2的正方形EFGH在边长为6的正方形ABCD所在平面上移动,始终保持EF∥AB.线段CF的中点为M,DH的中点为N,则线段MN的长为( )
 如图,边长为2的正方形EFGH在边长为6的正方形ABCD所在平面上移动,始终保持EF∥AB.线段CF的中点为M,DH的中点为N,则线段MN的长为( )
如图,边长为2的正方形EFGH在边长为6的正方形ABCD所在平面上移动,始终保持EF∥AB.线段CF的中点为M,DH的中点为N,则线段MN的长为( )| A. | $\sqrt{10}$ | B. | $\frac{\sqrt{17}}{2}$ | C. | $\sqrt{17}$ | D. | $\frac{4}{3}$$\sqrt{10}$ |
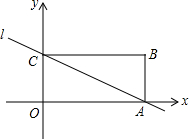 矩形ABCD在平面直角坐标系中,且顶点O为坐标原点,已知点B(3,2),则对角线AC所在的直线l对应的解析式为y=-$\frac{2}{3}$x+2.
矩形ABCD在平面直角坐标系中,且顶点O为坐标原点,已知点B(3,2),则对角线AC所在的直线l对应的解析式为y=-$\frac{2}{3}$x+2.