题目内容
 如图所示,直线AB与坐标轴交于A、B两点.
如图所示,直线AB与坐标轴交于A、B两点.现有五张正面分别写着连续自然数1、2、3、4、5的卡片,这五张卡片背面完全相同.将这五张卡背面朝上洗匀后随机抽取一张,以正面的数字作为x值.放回卡片再洗匀,再从中取出一张卡片,正面数字作为y值.
(1)用适当方法求出两次取出的卡片的数字的和是偶数的概率;
(2)若记P(x,y),分别求出P在直线上和P在△AOB内(不含边界)的概率.
考点:列表法与树状图法,一次函数的性质,待定系数法求一次函数解析式
专题:
分析:(1)根据题意画出树状图,然后根据树状图即可求得所有等可能的结果与卡片正面上的数字之和为偶数的情况,然后利用概率公式求解即可求得答案;
(2)根据(1)中的树状图即可求得所有等可能的结果然后利用概率公式求解即可求得答案.
(2)根据(1)中的树状图即可求得所有等可能的结果然后利用概率公式求解即可求得答案.
解答:解:(1)画树形图得:

所以两次取出的卡片的数字的和是偶数的概率=
;
(2)设直线的解析式为y=kx+b,
把(5,0)和(0,5)坐标代入求出k=-1,b=5,
则y=-x+5,
当P点的坐标为(1,4)、(2,3)、(3,2)、(4,1)时点P在直线上,
则P在直线上的概率为
;
当P的坐标分别为(1,1)、(1,2)(1,3)(1,4)、(2,1)、(2,2)、(2,4)、(3,1)、(4,2)、(4,3)时则P在△AOB内(不含边界),
则P在△AOB内(不含边界)的概率=
=
.

所以两次取出的卡片的数字的和是偶数的概率=
| 13 |
| 25 |
(2)设直线的解析式为y=kx+b,
把(5,0)和(0,5)坐标代入求出k=-1,b=5,
则y=-x+5,
当P点的坐标为(1,4)、(2,3)、(3,2)、(4,1)时点P在直线上,
则P在直线上的概率为
| 4 |
| 25 |
当P的坐标分别为(1,1)、(1,2)(1,3)(1,4)、(2,1)、(2,2)、(2,4)、(3,1)、(4,2)、(4,3)时则P在△AOB内(不含边界),
则P在△AOB内(不含边界)的概率=
| 10 |
| 25 |
| 2 |
| 5 |
点评:此题考查了树状图法与列表法求概率.此题难度不大,解题的关键是根据题意画出树状图或列出表格,注意树状图法与列表法可以不重不漏的表示出所有等可能的结果,注意用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
若(k-1)x|k|+20=0是一元一次方程,则k的值是( )
| A、1 | B、-1 | C、0 | D、±1 |
| ||
| y2+y+1 |
| (y-2)2 |
| x2+x+1 |
| A、-1 | B、0 | C、2 | D、1 |
计算(-4a3)2的结果是( )
| A、16a6 |
| B、-16a6 |
| C、8a6 |
| D、16a5 |
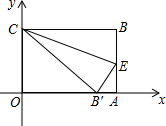 如图,在直角坐标系中放入一个边长OC为9的矩形纸片ABCO.将纸片翻折后,点B恰好落在x轴上,记为B′,折痕为CE,已知tanOB′C=
如图,在直角坐标系中放入一个边长OC为9的矩形纸片ABCO.将纸片翻折后,点B恰好落在x轴上,记为B′,折痕为CE,已知tanOB′C= △ABC中,∠B=90°,BD是斜边AC上的高. 求证:BD2=AD•CD.
△ABC中,∠B=90°,BD是斜边AC上的高. 求证:BD2=AD•CD.