题目内容
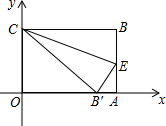 如图,在直角坐标系中放入一个边长OC为9的矩形纸片ABCO.将纸片翻折后,点B恰好落在x轴上,记为B′,折痕为CE,已知tanOB′C=
如图,在直角坐标系中放入一个边长OC为9的矩形纸片ABCO.将纸片翻折后,点B恰好落在x轴上,记为B′,折痕为CE,已知tanOB′C=| 3 |
| 4 |
考点:一次函数综合题
专题:
分析:先由tan∠OB′C=
,OC=9,利用三角函数即可求得OB′长,故可得出B′的坐标,由题意可知C(0,9),由勾股定理可得B'C的长,也就求得了OA长,那么利用直角三角形AB'E就能求得AE长,进而求得E的坐标,把这两点代入一次函数解析式即可.
| 3 |
| 4 |
解答::解:∵在Rt△B′OC中,tan∠OB′C=
,OC=9,
∴
=
,解得OB′=12,即点B′的坐标为(12,0).
∵将纸片翻折后,点B恰好落在x轴上的B′点,CE为折痕,
∴△CBE≌△CB′E,
∴BE=B′E,CB′=CB=OA,
在Rt△OB′C中,CB′=
=15,
设AE=a,则EB′=EB=9-a,AB′=AO-OB′=15-12=3,
在Rt△AEB′中,由勾股定理,
∵AE2+AB′2=B′E2,
∴a2+32=(9-a)2,解得a=4,
∴点E的坐标为(15,4),点C的坐标为(0,9),
设直线CE的解析式为y=kx+b(k≠0),根据题意得
,解得
,
∴CE所在直线的解析式为y=-
x+9.
| 3 |
| 4 |
∴
| 9 |
| OB′ |
| 3 |
| 4 |
∵将纸片翻折后,点B恰好落在x轴上的B′点,CE为折痕,
∴△CBE≌△CB′E,
∴BE=B′E,CB′=CB=OA,
在Rt△OB′C中,CB′=
| OB′2+OC2 |
设AE=a,则EB′=EB=9-a,AB′=AO-OB′=15-12=3,
在Rt△AEB′中,由勾股定理,
∵AE2+AB′2=B′E2,
∴a2+32=(9-a)2,解得a=4,
∴点E的坐标为(15,4),点C的坐标为(0,9),
设直线CE的解析式为y=kx+b(k≠0),根据题意得
|
|
∴CE所在直线的解析式为y=-
| 1 |
| 3 |
点评:本题考查的是一次函数综合题,涉及到图形反折变换的性质、勾股定理及用待定系数法求一次函数的解析式等知识,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列条件中不能确定是等腰三角形的是( )
| A、三条边都相等的三角形 |
| B、有一个锐角是45°的直角三角形 |
| C、一个外角的平分线平行于三角形一边的三角形 |
| D、一条中线把面积分成相等的两部分的三角形 |
 如图,在△ABC中,∠ACB=90°,CD为边AB上的高,已知BD=1,则线段AD的长是( )
如图,在△ABC中,∠ACB=90°,CD为边AB上的高,已知BD=1,则线段AD的长是( )| A、sin2A |
| B、cos2A |
| C、tan2A |
| D、cot2A |
 如图,已知:△ABC中,AB=AC,且⊙O内切于△ABC、D、E、F是切点,又CF交圆于G,EG延长交BC于M,AG交圆于K.
如图,已知:△ABC中,AB=AC,且⊙O内切于△ABC、D、E、F是切点,又CF交圆于G,EG延长交BC于M,AG交圆于K.(1)求证:△MCG∽△MEC;
(2)若EM⊥CD,求cos∠FAK的值.
函数y=
的自变量x的取值范围是( )
| x-2 |
| A、x为任意实数 | B、x≤2 |
| C、x≥2 | D、x>2 |
 如图,半径为1的圆片与数轴相切于原点,将该圆片沿数轴向负方向滚动一周,点A从原点到达点A′的位置,则数轴上点A′对应的实数为
如图,半径为1的圆片与数轴相切于原点,将该圆片沿数轴向负方向滚动一周,点A从原点到达点A′的位置,则数轴上点A′对应的实数为 如图所示,直线AB与坐标轴交于A、B两点.
如图所示,直线AB与坐标轴交于A、B两点.