Question

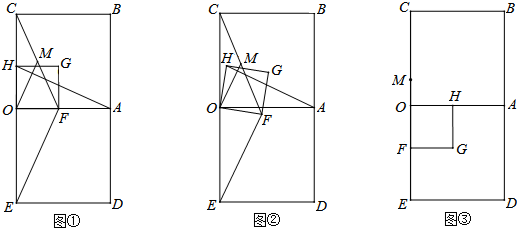
如图，已知直线l：y=kx+b（k，b为常数，且k≠0）与x轴，y轴分别交于点C，B两点．⊙A的圆心在x轴上，与x轴交于D，E两点，且与直线l相切于点B．作矩形OBGF，使得点G在⊙A上，F在x轴上．
（1）填空：用k，b表示点的坐标：C

 

；B

 

；A

 

； 
（2）当矩形OBGF是正方形时，求k的值； 
（3）在（2）的前提下，有一条抛物线y=ax²+mx+c（a，m，c均为常数，其中a≠0），经过点D，E两点，且顶点H，在弓形BG内（包括边界

BG

和弦BG），当

5

≤b≤5，请你求出a的范围．

Answer 1

考点：圆的综合题,不等式的性质,勾股定理,矩形的判定与性质,正方形的性质,垂径定理,切线的性质,相似三角形的判定与性质

专题：综合题

分析：（1）连接AB，根据直线与坐标轴交点的坐标特征可用k、b的代数式表示点C、B的坐标；然后通过证明△AOB∽△BOC，就可求出OA长，从而得到点A的坐标．
（2）过点A作BG的垂线，交BG于点M，交⊙A于点N，连接AB，由垂径定理可得BM=GM，易证四边形OBMA是矩形，从而得到OA=BM=

1

2

BG=

1

2

OB=

b

2

，而OA=kb，就可求出k的值．
（3）在（2）的条件下可以用b的代数式表示点D、E的坐标，然后将抛物线的解析式设成交点式，再转化为一般式，就可用a、b的代数式表示出顶点H的坐标，由于顶点H在线段MN之间，从而可以得到关于a、b的不等式组，然后利用条件“

5

≤b≤5”及不等式的性质就可求出a的取值范围．

解答：解：（1）连接AB，如图1，
由kx+b=0得x=-

b

k

，则点C的坐标为（-

b

k

，0），OC=

b

k

．
由x=0得y=b，则点B的坐标为（0，b），OB=b．
∵BC与⊙A相切于点B，
∴AB⊥BC，即∠ABC=90°．
∵∠AOB=90°，
∴∠ABO=90°-∠CBO=∠BCO．
∵∠AOB=∠BOC=90°，
∴△AOB∽△BOC．
∴

OA

OB

=

OB

OC

．
∴OB²=OA•OC．
∴b²=OA•

b

k

．
∴OA=kb．
∴点A的坐标为（kb，0）．
故答案分别为：（-

b

k

，0），（0，b），（kb，0）．

（2）过点A作BG的垂线，交BG于点M，交⊙A于点N，连接AB，如图2，
则有AB=AN，BM=GM=

1

2

BG．
∵四边形OBGF是正方形，
∴BG=OB=b．
∴BM=

1

2

b．
∵∠OBG=∠BOE=∠BMA=90°，
∴四边形OBMA是矩形．
∴AM=OB=b，OA=BM=

1

2

b．
∵OA=kb，∴kb=

1

2

b．
∵b≠0，∴k=

1

2

．
∴k的值为

1

2

．

（3）如图2，
∵∠AOB=90°，OA=

1

2

b，OB=b，
∴AN=AB=

OA2+OB2

=

5 b

2

．
∴AD=AE=AB=

5 b

2

．
∴点D的坐标为（

1- 5

2

b，0），点E的坐标为（

1+ 5

2

b，0）．
可设过点D、E的抛物线的解析式为y=a（x-

1- 5

2

b）（x-

1+ 5

2

b）
则有y=ax²-abx-ab²．
则顶点H的坐标为（-

-ab

2a

，

4a•(-ab2)-(-ab)2

4a

），即H（

b

2

，

-5ab2

4

）．
由题可知：点H在线段MN上，
则b≤

-5ab2

4

≤

5 b

2

．
∵b＞0，∴-5b²＜0．
∴-

1

5b

≥

a

4

≥-

5

10b

，即-

5

10b

≤

a

4

≤-

1

5b

．
∵

5

≤b≤5，
∴

5

5

≥

1

b

≥

1

5

．
∴-

5

5

≤-

1

b

≤-

1

5

．
∴-

1

5b

≤-

1

25

，
-

5

10b

≥-

5

5

×

5

10

=-

1

10

．
∴-

1

10

≤-

5

10b

≤

a

4

≤-

1

5b

≤-

1

25

，
∴-

1

10

≤

a

4

≤-

1

25

．
∴-

2

5

≤a≤-

4

25

．
∴a的取值范围为-

2

5

≤a≤-

4

25

．

点评：本题考查了圆的切线的性质、垂径定理、相似三角形的判定与性质、矩形的判定与性质、正方形的性质、不等式的性质、勾股定理等知识，有一定的综合性，而灵活使用不等式的性质是解决第三小题的关键．