题目内容
【题目】已知抛物线y1＝x2与直线
相交于A、B两点
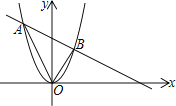
(1)求A、B两点的坐标
(2)点O为坐标原点，△AOB的面积等于___________
(3)当y1＜y2时，x的取值范围是________________
【答案】（1）A(2,4),B(
,
)；（2）
；（3）2<x<.
【解析】
（1）根据解方程组，可得交点坐标；
（2）根据面积的和差，可得答案；
（3）结合函数图象根据函数与不等式的关系，可得答案．
(1)联立抛物线y1=x2与直线
，得
，
解得
,
，
A(2,4),B(,)；
(2)当y=0时,
x+3=0，解得x=6，
即C(6,0).
S△AOB=S△AOCS△BOC=×6×4×6×
；
(3)结合函数图象抛物线在直线的下方，得2<x<.
练习册系列答案
名校课堂系列答案
相关题目
