Question

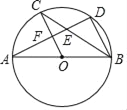
【题目】如图，∠BAC=60°，AD平分∠BAC交⊙O于点D，连接OB、OC、BD、CD．

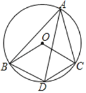
（1）求证：四边形OBDC是菱形；

（2）当∠BAC为多少度时，四边形OBDC是正方形？

Answer 1

【答案】（1）详见解析；（2）当∠BAC为45度时，四边形OBDC是正方形，理由详见解析.

【解析】

（1）连接OD，由AD平分∠BAC可求得∠BAD=∠DAC=30°，再根据同弧所对的圆周角是圆心角的一半可知∠BOD=∠DOC=60°，从而求得△BOD和△COD都是等边三角形，即可得出结论.

（2）若使菱形为正方形则只需使一个内角为90°即可，可求得∠BAC 为45°.

（1）证明：连接OD，

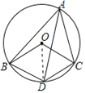
∵∠BAC=60°，AD平分∠BAC

∴∠BAD=∠DAC=30°，

∴∠BOD=∠COD=60°，

由圆半径相等可知OB=OD=OC，

∴△BOD和△COD都是等边三角形，

∴OB=BD=DC=OC，

∴四边形OBDC是菱形；

（2）解：当∠BAC为45度时，四边形OBDC是正方形，

理由是：若∠BAC=45°，

则∠BOC=90°，

∵四边形OBDC是菱形，

∴四边形OBDC是正方形．