题目内容
5.已知m<1,且a=-m2+2m-1,那么( )| A. | a>0 | B. | a≥0 | C. | a<0 | D. | a≤0 |
分析 已知等式配方后,利用非负数的性质确定出范围即可.
解答 解:∵m<1,
∴a=-m2+2m-1=-(m-1)2<0,
故选C.
点评 此题考查了配方法的应用,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
相关题目
8.在函数y=-$\frac{{a}^{2}+1}{x}$(a为常数)的图象上有点A(-1,y1),B($\frac{1}{4}$,y2),C($\frac{1}{2}$,y3),则函数值y1,y2,y3的大小关系是( )
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y2<y3<y1 | D. | y2<y1<y3 |
13.若最简二次根式3$\sqrt{5}$与-5$\sqrt{x}$可以合并,则x的值是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
14.下列方程中,有实数根的方程是( )
| A. | $\sqrt{{x}^{2}+1}=0$ | B. | $\sqrt{x-2}+\frac{1}{2}=0$ | C. | $\sqrt{x+1}=2$ | D. | $\sqrt{x-1}+\sqrt{1-x}=2$ |
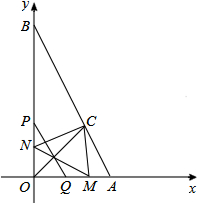 如图,已知△OAB和△OQP在平面直角坐标系中,A(2,0),B(0,4),P为从O点出发,以每秒2个单位长的速度沿x轴向点B作匀速运动的动点,且PQ∥AB,PQ交x轴于点Q,∠AOB的平分线交AB于C,设P运动的时间为t(0<t<2)秒.
如图,已知△OAB和△OQP在平面直角坐标系中,A(2,0),B(0,4),P为从O点出发,以每秒2个单位长的速度沿x轴向点B作匀速运动的动点,且PQ∥AB,PQ交x轴于点Q,∠AOB的平分线交AB于C,设P运动的时间为t(0<t<2)秒.