题目内容
16.三元一次方程组$\left\{\begin{array}{l}{3x-y+z=4}\\{2x+3y-z=12}\\{x+y+z=6}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=3}\\{z=1}\end{array}\right.$.分析 可用减法化去y,达到消元的目的,然后解关于x、z的方程组.
解答 解:组$\left\{\begin{array}{l}{3x-y+z=4(1)}\\{2x+3y-z=12(2)}\\{x+y+z=6(3)}\end{array}\right.$,
由(1)+(3),得
4x+2z=10,(4)
由(1)×3+(2),得
11x+2z=24,(5)
由(5)-(4),解得x=2.
将其代入(5),解得z=1,
把x=2,z=1代入(1),解得y=3.
所以原方程组的解为:$\left\{\begin{array}{l}{x=2}\\{y=3}\\{z=1}\end{array}\right.$.
故答案是:$\left\{\begin{array}{l}{x=2}\\{y=3}\\{z=1}\end{array}\right.$.
点评 本题考查三元一次方程组的解法,解决本题关键是寻找式子间的关系,寻找方法降元.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
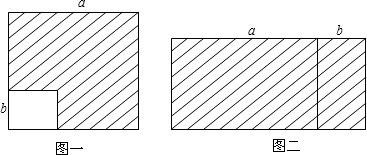
4.如图(一),在边长为a的正方形中,挖掉一个边长为b的小正方形(a>b),把余下的部分剪成一个矩形(如图(二)),通过计算两个图形(阴影部分)的面积,验证了一个等式,则这个等式是( )

| A. | (a+b)2=a2+2ab+b2 | B. | a2-b2=(a+b)(a-b) | ||
| C. | (a-b)2=a2-2ab+b2 | D. | (a+2b)(a-b)=a2+ab-2b2 |
6.二元一次方程2x+y=4的自然数解有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |

 解不等式组3x-1<2(x+1)并把解集在数轴上表示出来.
解不等式组3x-1<2(x+1)并把解集在数轴上表示出来.