题目内容
6. 若二次函数y=-ax2+2ax+3的部分图象如图所示,则一元二次方程-ax2+2ax+3=0的根为x1=3;x2=-1.
若二次函数y=-ax2+2ax+3的部分图象如图所示,则一元二次方程-ax2+2ax+3=0的根为x1=3;x2=-1.
分析 由抛物线与x轴的一个交点为(3,0)可知一元二次方程-ax2+2ax+3=0的一个根为3,再设方程的另一个根为x,根据根与系数的关系即可求出x的值.
解答 解:∵二次函数y=-ax2+2ax+3的图象x轴的一个交点为(3,0),
∴一元二次方程-ax2+2ax+3=0一个根为3,
∴设方程的另一个根为x,则x+3=-$\frac{2a}{-a}$=2,解得x=-1,
∴一元二次方程-ax2+2ax+3=0的根为3,-1.
故答案为:3,-1.
点评 本题考查的是抛物线与x轴的交点问题,根据抛物线与x轴的交点求出一元二次方程的一个根是解答此题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
11.小张笔记上有一道练习题(8a2+3ab-2b2)-(-2a2+ab-3b2)=10a2______+b2但空格处被墨水污染了,请问被污染的一项是( )
| A. | -2ab | B. | +2ab | C. | +4ab | D. | -4ab |
16.下列各组不是同类项的是( )
| A. | a2b3与-5a2b3 | B. | $\frac{1}{2}$xy2与4y2x | C. | 2x2y与2xy2 | D. | -3与π |

 已知△ABC,求作△DEF,使△DEF≌△ABC(尺规作图,保留作图痕迹).
已知△ABC,求作△DEF,使△DEF≌△ABC(尺规作图,保留作图痕迹).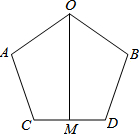 已知:OA=OB,AC=BD,∠A=∠B,M为CD中点.求证:OM平分∠AOB.
已知:OA=OB,AC=BD,∠A=∠B,M为CD中点.求证:OM平分∠AOB.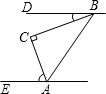 如图,在△ABC中,∠C=90°.若BD∥AE,则∠DBC+∠CAE的度数是90°.
如图,在△ABC中,∠C=90°.若BD∥AE,则∠DBC+∠CAE的度数是90°.