题目内容
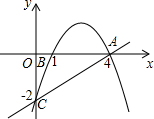 如图,已知抛物线y=ax2+bx-2经过A(4,0),B(1,0)两点.
如图,已知抛物线y=ax2+bx-2经过A(4,0),B(1,0)两点.(1)求出抛物线的解析式;
(2)若抛物线与直线y=
| 1 |
| 2 |
(3)P是抛物线上一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以A,P,M为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)本题需先根据图象过A,B两点,即可得出解析式.
(2)抛物线与直线有交点,联立两直线方程求解,△≥0,即可求得c的取值范围.
(3)本题首先判断出存在,首先设出横坐标和纵坐标,从而得出PA的解析式,再分三种情况进行讨论,当
=
=
时和当
=
=
时,得出△APM∽△ACO△APM∽△CAO,分别求出点P的坐标即可.
(2)抛物线与直线有交点,联立两直线方程求解,△≥0,即可求得c的取值范围.
(3)本题首先判断出存在,首先设出横坐标和纵坐标,从而得出PA的解析式,再分三种情况进行讨论,当
| AM |
| PM |
| AO |
| OC |
| 2 |
| 1 |
| AM |
| PM |
| AO |
| OC |
| 1 |
| 2 |
解答:解:(1)将A(4,0),B(1,0)的坐标代入y=ax2+bx-2得
,
解得
,
故此抛物线的解析式为y=-
x2+
x-2.
(2)
有交点,
即
x+c=-
x2+
x-2,化简为
x2-2x+2+c=0,
△≥0,即22-4×
×(2+c)≥0,
解得c≤0.
(3)存在.
设点P的横坐标为m,则P的纵坐标为-
m2+
m-2,
AM=4-m,PM=-
m2+
m-2,
又∵∠COA=∠PMA=90°,
∴①当
=
=
时,
△APM∽△ACO,
即4-m=2(-
m2+
m-2)
解得:m1=2,m2=4(舍去),
则P(2,1),
②当
=
=
时,
△APM∽△CAO,
即2(4-m)=-
m2+
m-2,
解得:m1=4,m2=5(均不合题意,舍去),
故符合条件的点P的坐标为P(2,1).
|
解得
|
故此抛物线的解析式为y=-
| 1 |
| 2 |
| 5 |
| 2 |
(2)
|
即
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
△≥0,即22-4×
| 1 |
| 2 |
解得c≤0.
(3)存在.
设点P的横坐标为m,则P的纵坐标为-
| 1 |
| 2 |
| 5 |
| 2 |
AM=4-m,PM=-
| 1 |
| 2 |
| 5 |
| 2 |
又∵∠COA=∠PMA=90°,
∴①当
| AM |
| PM |
| AO |
| OC |
| 2 |
| 1 |
△APM∽△ACO,
即4-m=2(-
| 1 |
| 2 |
| 5 |
| 2 |
解得:m1=2,m2=4(舍去),
则P(2,1),
②当
| AM |
| PM |
| AO |
| OC |
| 1 |
| 2 |
△APM∽△CAO,
即2(4-m)=-
| 1 |
| 2 |
| 5 |
| 2 |
解得:m1=4,m2=5(均不合题意,舍去),
故符合条件的点P的坐标为P(2,1).
点评:本题考查了抛物线解析式的求法,两曲线相交转化为根判别式求解,抛物线与相似三角形的问题,综合性较强,是一道好题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 (1)在数轴上近似地表示下列各数,4,-1.5,0,
(1)在数轴上近似地表示下列各数,4,-1.5,0,