题目内容
如图,△ABC的三个顶点 都在⊙O上,AP⊥BC于P,AM为⊙O的直径.
都在⊙O上,AP⊥BC于P,AM为⊙O的直径.
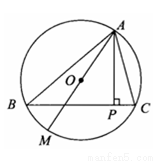
求证:∠BAM=∠CAP.
证明:连接BM,
∵AM为⊙O的直径,
∴∠ABM=90°,
∴∠M+∠BAM=90°,
∵AP⊥BC,
∴∠APC=90°,
∴∠C+∠CAP=90°,
∵∠C=∠M,
∴∠BAM=∠CAP.
【解析】
试题分析:首先连接BM,根据同弧所对圆周角相等,即可得∠C=∠M,由AM为⊙O的直径,根据
圆周角定理,即可得∠ABM=90°,又由AP⊥BC,利用等角的余角相等,即可证得∠BAM=∠CAP.
考点:圆周角定理

练习册系列答案
相关题目
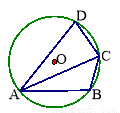
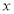 轴、
轴、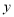 轴分别相交于A、B两点,且与反比例函数的图象在第二象限交于点C.如果点A的坐标为
轴分别相交于A、B两点,且与反比例函数的图象在第二象限交于点C.如果点A的坐标为 ,OA=2OB,点 B是AC的中点.
,OA=2OB,点 B是AC的中点.

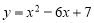 的最大值.他画图研究后发现,
的最大值.他画图研究后发现,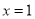 和
和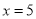 时的函数值相等,于是他认为需要对
时的函数值相等,于是他认为需要对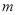 进行分类讨论.他的解答过程如下:
进行分类讨论.他的解答过程如下:
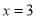 ,
,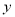 的最大值为2;
的最大值为2;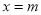 时,
时,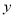 的最大值为
的最大值为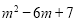 .
.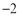 ≤x≤4时,二次函数
≤x≤4时,二次函数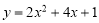 的最大值为_______;
的最大值为_______;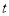 的值为_______.
的值为_______.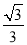 x,点A1坐标为(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O 为圆心,OB1长为半径画弧交y一轴于点A2;再过点A2作y轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交y轴于点A3,…,按此做法进行下去,点A4的坐标为(_______,_______);点An的坐标为(_______,_______).
x,点A1坐标为(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O 为圆心,OB1长为半径画弧交y一轴于点A2;再过点A2作y轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交y轴于点A3,…,按此做法进行下去,点A4的坐标为(_______,_______);点An的坐标为(_______,_______).
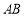 为⊙
为⊙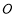 的直径,弦
的直径,弦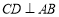 ,垂足为点
,垂足为点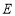 ,连结
,连结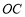 ,若
,若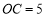 ,
,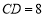 ,则
,则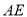 的长为( )
的长为( )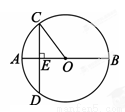
 B.4 C.3 D.2
B.4 C.3 D.2 是二次函数,那么a=__________.
是二次函数,那么a=__________. 时,求下列各代数式的值:
时,求下列各代数式的值: (2)
(2)