题目内容
3.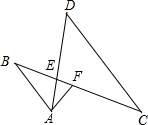 已知:如图,AB∥CD,AD、BC交于点E,F为BC上一点,且∠EAF=∠C.
已知:如图,AB∥CD,AD、BC交于点E,F为BC上一点,且∠EAF=∠C.(1)求证:△AEF∽△BAF;
(2)若EF=2,BE=4,求AF.
分析 (1)根据平行线的性质和等量关系可得∠EAF=∠B,再由公共角,由AA可证△AEF∽△BAF;
(2)根据相似三角形的性质可得$\frac{AF}{BF}=\frac{EF}{AF}$,再代入数据计算即可求解.
解答 (1)证明:∵AB∥CD,
∴∠B=∠C,
∵∠EAF=∠C,
∴∠EAF=∠B,
又∵∠EFA=∠EFA,
∴△AEF∽△BAF;
(2)解:由(1)得$\frac{AF}{BF}=\frac{EF}{AF}$,
∴AF2=FE•FB=12,
∴AF2=2$\sqrt{3}$.
点评 主要考查了相似三角形的判定及其性质的应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.若点A(a,2-a)在第一象限,a为整数,则a的平方根是( )
| A. | 1 | B. | ±2 | C. | ±1 | D. | 不确定 |
8.已知关于x的方程(k-3)x|k|-1+(2k-3)x+4=0是一元二次方程,则k的值应为( )
| A. | ±3 | B. | 3 | C. | -3 | D. | 不能确定 |
12.若关于x的方程3x+3a=2的解是正数,则a的取值范围是( )
| A. | a≤$\frac{2}{3}$ | B. | a≥$\frac{2}{3}$ | C. | a>$\frac{2}{3}$ | D. | a<$\frac{2}{3}$ |