题目内容
15.若一元二次方程mx2+4x+5=0有两个不相等实数根,则m的取值范围m<$\frac{4}{5}$且m≠0.分析 由一元二次方程mx2+4x+5=0有两个不相等实数根,可得△=b2-4ac>0且m≠0,解此不等式组即可求得答案.
解答 解:∵一元二次方程mx2+4x+5=0有两个不相等实数根,
∴△=b2-4ac=42-4×m×5=16-20m>0,
解得:m<$\frac{4}{5}$,
∵m≠0,
∴m的取值范围为:m<$\frac{4}{5}$ 且m≠0.
故答案为:m<$\frac{4}{5}$ 且m≠0.
点评 此题考查了根的判别式.注意△>0?方程有两个不相等的实数根.

练习册系列答案
相关题目
10.若关于x的一元二次方程(m-1)x2-2x+1=0有两个不相等的实数根,则m的取值范围是( )
| A. | m<2且m≠1 | B. | m>2 | C. | m<-2 | D. | m<2 |
7. 如图,已知二次函数y=x2+bx+3的图象与x轴正半轴交于B、C两点,BC=2,则b的值为( )
如图,已知二次函数y=x2+bx+3的图象与x轴正半轴交于B、C两点,BC=2,则b的值为( )
 如图,已知二次函数y=x2+bx+3的图象与x轴正半轴交于B、C两点,BC=2,则b的值为( )
如图,已知二次函数y=x2+bx+3的图象与x轴正半轴交于B、C两点,BC=2,则b的值为( )| A. | 4 | B. | -4 | C. | ±4 | D. | -5 |
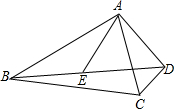 如图,已知:∠ACB=∠ADE,∠ABC=∠AED,求证:△ABE∽△ACD.
如图,已知:∠ACB=∠ADE,∠ABC=∠AED,求证:△ABE∽△ACD.
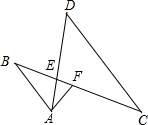 已知:如图,AB∥CD,AD、BC交于点E,F为BC上一点,且∠EAF=∠C.
已知:如图,AB∥CD,AD、BC交于点E,F为BC上一点,且∠EAF=∠C.