题目内容
16.已知:x2+3x+1=0.求(1)x+$\frac{1}{x}$;
(2)x2+$\frac{1}{{x}^{2}}$.
分析 (1)把方程两边除以x即可得到x+$\frac{1}{x}$=-3;
(2)先利用完全平方公式得到x2+$\frac{1}{{x}^{2}}$=(x+$\frac{1}{x}$)2-2,然后把(1)中的计算结果代入计算即可.
解答 解:(1)∵x2+3x+1=0,
而x≠0,
∴x+3+$\frac{1}{x}$=0,
∴x+$\frac{1}{x}$=-3;
(2)x2+$\frac{1}{{x}^{2}}$=(x+$\frac{1}{x}$)2-2=(-3)2-2=7.
点评 本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.也考查了代数式的变形能力.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案
相关题目
1.下列各式中正确的是( )
| A. | -3(a-7)=-3a-21 | B. | 3a-(4a2+2)=3a-4a2+2 | ||
| C. | -[-(2a+3y)]=2a-3y | D. | -2x-y=-(2x+y) |
 如图,在△ABC中,∠BAC的平分线与∠ABC外角的平分线交于点F,∠ABC的平分线与AF交于点D,若∠C=80°,求∠F的度数.
如图,在△ABC中,∠BAC的平分线与∠ABC外角的平分线交于点F,∠ABC的平分线与AF交于点D,若∠C=80°,求∠F的度数.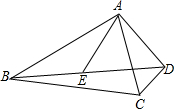 如图,已知:∠ACB=∠ADE,∠ABC=∠AED,求证:△ABE∽△ACD.
如图,已知:∠ACB=∠ADE,∠ABC=∠AED,求证:△ABE∽△ACD.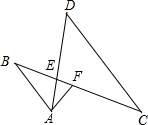 已知:如图,AB∥CD,AD、BC交于点E,F为BC上一点,且∠EAF=∠C.
已知:如图,AB∥CD,AD、BC交于点E,F为BC上一点,且∠EAF=∠C.