题目内容
在梯形ABCD中，已知AB∥CD，∠ABC=90°，BD⊥AD，BC=6，BD=13．则梯形ABCD的面积为 ．
考点：梯形
专题：
分析：如图，作辅助线，首先求出DC的长度，进而运用射影定理求出AE的长度，即可解决问题．
解答：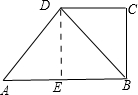
解：如图，过点D作DE⊥AB于点E；
则四边形DEBC为矩形；
∴DE=BC=6，BE=DC；
∵AB∥CD，∠ABC=90°，
∴∠BCD=90°，
由勾股定理得：
DC2=BD2-BC2=132-62，
∴DC=
；
∵BD⊥AD，
∴由射影定理得：DE2=AE•BE，
即62=AE×
，
∴AE=
，
∴梯形ABCD的面积=
(
+
+
)×6
=
．
解：如图，过点D作DE⊥AB于点E；则四边形DEBC为矩形；
∴DE=BC=6，BE=DC；
∵AB∥CD，∠ABC=90°，
∴∠BCD=90°，
由勾股定理得：
DC2=BD2-BC2=132-62，
∴DC=
| 133 |
∵BD⊥AD，
∴由射影定理得：DE2=AE•BE，
即62=AE×
| 133 |
∴AE=
| 36 | ||
|
∴梯形ABCD的面积=
| 1 |
| 2 |
| 133 |
| 133 |
| 36 | ||
|
=
906
| ||
| 133 |
点评：该题以梯形为载体，考查了梯形的性质、勾股定理及其应用问题；解题的关键是作辅助线，灵活运用勾股定理等几何知识来分析、求解、推理或解答．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
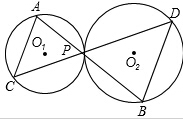如图，已知⊙O1和⊙O2外切于点P，过点P．作直线AB、CD，AB分别交⊙O1和⊙O2于点A、B，CD分别交⊙O1和⊙O2于C、D两点，求证：AC∥BD．
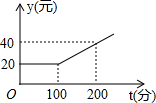已知甲、乙两家通信公司都推出了市话通话优惠业务，甲公司每月的市话费标准如图所示，乙公司每月通话收费标准如表所示．
如图所示，直线AB、CD相交于点O，OE是∠AOD的平分线，∠FOC=90°，∠1=70°，求∠2与∠3的度数．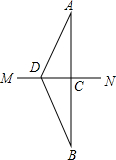
如图，A、B两个村庄在河MN的两侧，连接AB，与MN相交于点C，点D在MN上，连接AD、BD，且AD=BD，若要在河上建一座桥，使A、B两村来往最便捷，则应该把桥建在点C还是点D？为什么？
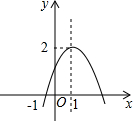如图，已知二次函数y=ax2+bx+c（a≠0）图象过点（-1，0），顶点为（1，2），则结论：