题目内容
△ABC中,∠BAC是直角,过斜边中点M而垂直于斜边BC的直线交CA的延长线于E,交AB于D,连AM.求证:
(1)△MAD∽△MEA
(2)AM2=MD•ME.
(1)△MAD∽△MEA
(2)AM2=MD•ME.
考点:相似三角形的判定与性质
专题:
分析:(1)首先证明∠E=∠B,进而证明∠AMD=∠EMA,问题即可解决.
(2)由△MAD∽△MEA,写出比例式问题即可解决.
(2)由△MAD∽△MEA,写出比例式问题即可解决.
解答: 证明:(1)∵∠BAC是直角,ME⊥BC,
证明:(1)∵∠BAC是直角,ME⊥BC,
∴∠C+∠E=∠C+∠B,
∴∠E=∠B;
∵点M为直角△ABC斜边的中点,
∴MA=MB,∠MAD=∠B;
而∠AMD=∠EMA,
∴△MAD∽△MEA.
(2)∵△MAD∽△MEA,
∴
=
,
∴AM2=MD•ME.
 证明:(1)∵∠BAC是直角,ME⊥BC,
证明:(1)∵∠BAC是直角,ME⊥BC,∴∠C+∠E=∠C+∠B,
∴∠E=∠B;
∵点M为直角△ABC斜边的中点,
∴MA=MB,∠MAD=∠B;
而∠AMD=∠EMA,
∴△MAD∽△MEA.
(2)∵△MAD∽△MEA,
∴
| AM |
| ME |
| MD |
| AM |
∴AM2=MD•ME.
点评:该题主要考查了相似三角形的判定及其性质定理的应用问题;解题的关键是深入分析、准确判断、科学论证.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
下面的图案中,不是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
一个数的相反数是这个数本身,这样的数的个数是( )
| A、0 | B、1 | C、2 | D、无数 |
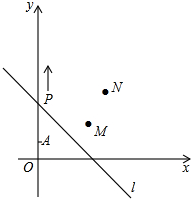 如图,A(0,2),M(4,3),N(5,6),动点P从点A出发,沿y轴以每秒1个单位长度的速度向上移动,且过点P的直线L:y=-x+b也随之平移,设移动时间为t秒,若点M,N位于直线L的异侧,则t的取值范围是
如图,A(0,2),M(4,3),N(5,6),动点P从点A出发,沿y轴以每秒1个单位长度的速度向上移动,且过点P的直线L:y=-x+b也随之平移,设移动时间为t秒,若点M,N位于直线L的异侧,则t的取值范围是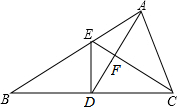 如图,已知△ABC中,D为BC中点,AD=AC,DE⊥BC,DE与AB交于E,EC与AD相交于点F,
如图,已知△ABC中,D为BC中点,AD=AC,DE⊥BC,DE与AB交于E,EC与AD相交于点F, 以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于D,过点D作⊙O的切线交BC于点E,连接OE.求证:EB=EC=ED.
以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于D,过点D作⊙O的切线交BC于点E,连接OE.求证:EB=EC=ED. 如图,∠DAB=∠CAE,AB•AD=AE•AC,则∠D=
如图,∠DAB=∠CAE,AB•AD=AE•AC,则∠D=