题目内容
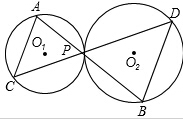 如图,已知⊙O1和⊙O2外切于点P,过点P.作直线AB、CD,AB分别交⊙O1和⊙O2于点A、B,CD分别交⊙O1和⊙O2于C、D两点,求证:AC∥BD.
如图,已知⊙O1和⊙O2外切于点P,过点P.作直线AB、CD,AB分别交⊙O1和⊙O2于点A、B,CD分别交⊙O1和⊙O2于C、D两点,求证:AC∥BD.考点:相切两圆的性质
专题:证明题
分析:如图,作两圆的公切线,运用弦切角定理证明∠ACD=∠BDC,即可解决问题.
解答: 解:如图,过点P作两圆的公切线MN;
解:如图,过点P作两圆的公切线MN;
则∠ACD=∠APM,∠BDC=∠BPN;
∵∠APM=∠BPN,
∴∠ACD=∠BDC,
∴AC∥BD.
 解:如图,过点P作两圆的公切线MN;
解:如图,过点P作两圆的公切线MN;则∠ACD=∠APM,∠BDC=∠BPN;
∵∠APM=∠BPN,
∴∠ACD=∠BDC,
∴AC∥BD.
点评:该题考查了相切两圆的性质及其应用问题;解题的关键是作公切线,灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
相关题目
一个数的相反数是这个数本身,这样的数的个数是( )
| A、0 | B、1 | C、2 | D、无数 |
 如图,∠DAB=∠CAE,AB•AD=AE•AC,则∠D=
如图,∠DAB=∠CAE,AB•AD=AE•AC,则∠D= 如图所示的正方体,一蚂蚁在A的位置,在G位置刚好有一颗糖,蚂蚁要想从顶点A经过它的表面到达顶点G,蚂蚁走哪一条路径最短?在图中画出你认为最短的路线.
如图所示的正方体,一蚂蚁在A的位置,在G位置刚好有一颗糖,蚂蚁要想从顶点A经过它的表面到达顶点G,蚂蚁走哪一条路径最短?在图中画出你认为最短的路线.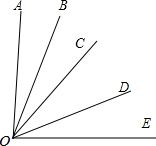 已知OB,OC,OD为∠AOE内三条射线.
已知OB,OC,OD为∠AOE内三条射线.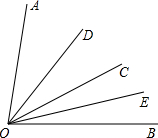 如图,已知∠DOC=25°,∠EOC=15°,OD平分∠AOC,OE平分∠BOC,求∠AOC、∠BOC、∠AOB的度数.
如图,已知∠DOC=25°,∠EOC=15°,OD平分∠AOC,OE平分∠BOC,求∠AOC、∠BOC、∠AOB的度数.