题目内容
 在△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB、BC于D、E.若∠CAB=∠B+30°,CE=2cm.求:
在△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB、BC于D、E.若∠CAB=∠B+30°,CE=2cm.求:(1)∠AEB的度数.
(2)BC的长.
考点:线段垂直平分线的性质,勾股定理
专题:
分析:(1)首先根据线段垂直平分线的性质可得AE=EB,根据等边对等角可得∠B=∠EAB,再由条件∠CAB=∠B+30°可得∠CAE=30°,进而可得∠CEA的度数,再利用平角定义可得答案.
(2)根据直角三角形30°角所对的直角边等于斜边的一半可得AE=2CE=4cm,再根据线段的和差关系可得答案.
(2)根据直角三角形30°角所对的直角边等于斜边的一半可得AE=2CE=4cm,再根据线段的和差关系可得答案.
解答:解:(1)∵DE垂直平分斜边AB,
∴AE=EB,
∴∠B=∠EAB,
 ∵∠CAB=∠B+30°,
∵∠CAB=∠B+30°,
∴∠CAE=30°,
∵∠C=90°,
∴∠CEA=60°,
∴∠AEB=120°;
(2)∵∠CAE=30°,
∴AE=2CE=4cm,
∴EB=4cm,
∴CB=4+2=6(cm).
∴AE=EB,
∴∠B=∠EAB,
 ∵∠CAB=∠B+30°,
∵∠CAB=∠B+30°,∴∠CAE=30°,
∵∠C=90°,
∴∠CEA=60°,
∴∠AEB=120°;
(2)∵∠CAE=30°,
∴AE=2CE=4cm,
∴EB=4cm,
∴CB=4+2=6(cm).
点评:此题主要考查了直角三角形的性质,以及线段垂直平分线的性质,关键是掌握垂直平分线上任意一点,到线段两端点的距离相等.

练习册系列答案
相关题目
下列计算正确的是( )
| A、(x-8y)(x-y)=x2-9xy+8y2 |
| B、(a-1)2=a2-1 |
| C、-x(x2+x-1)=-x3+x2-x |
| D、(x+y)(x2+xy+y2)=x3+y3 |
下列各式中,正确的是( )
| A、(-1)99=-99 |
| B、-(-22)=4 |
| C、-102=(-10)×(-10) |
| D、2-|-2|=4 |
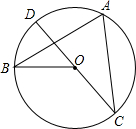 如图,CD是⊙O的直径,A,B是⊙O上任意两点,设∠BAC=y,∠BOD=x,则y与x之间的函数关系式是
如图,CD是⊙O的直径,A,B是⊙O上任意两点,设∠BAC=y,∠BOD=x,则y与x之间的函数关系式是 如图,已知抛物线y1=-2x2+2与直线y2=2x+2交于A、B两点
如图,已知抛物线y1=-2x2+2与直线y2=2x+2交于A、B两点