题目内容
具备下列条件的两个三角形中，不一定全等的是（ ）
| A、两角一边对应相等 |
| B、三边对应相等 |
| C、有两边一角对应相等 |
| D、有两边及其来夹角对应相等 |
考点：全等三角形的判定
专题：
分析：根据题意，可以采用排除法对各个选项进行分析，从而得出最后答案．
解答：解：A、两角一边对应相等，可以用AAS判定，故正确；
B、三边对应相等，符合SSS，故正确；
C、该角必须是两边的夹角才符合SAS判定，故错误；
D、两边和它们的夹角对应相等，符合SAS，故正确．
故选C．
B、三边对应相等，符合SSS，故正确；
C、该角必须是两边的夹角才符合SAS判定，故错误；
D、两边和它们的夹角对应相等，符合SAS，故正确．
故选C．
点评：本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、AAS、ASA、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．
练习册系列答案
阅读快车系列答案
相关题目
在“同一平面”条件下，下列说法中错误的个数是（ ）
（1）过一点有且只有一条直线与已知直线平行；
（2）过一点有且只有一条直线与已知直线垂直；
（3）平移只改变图形的位置，不改变图形的形状和大小；
（4）有公共顶点且有一条公共边的两个角互为邻补角．
（1）过一点有且只有一条直线与已知直线平行；
（2）过一点有且只有一条直线与已知直线垂直；
（3）平移只改变图形的位置，不改变图形的形状和大小；
（4）有公共顶点且有一条公共边的两个角互为邻补角．
| A、1个 | B、2个 | C、3个 | D、4个 |
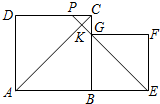如图，把边长分别为8cm和6cm的两个正方形ABCD与BEFG并排放在一起，直线EG交DC于P，AC交PG于K，则△AEK的面积是（ ）| A、51cm2 |
| B、50cm2 |
| C、49cm2 |
| D、48cm2 |
（1）绝对值等于它本身的数只有正数；
（2）平方根等于它本身的数有1和0；
（3）倒数等于它本身的数有±1，0；
（4）立方根等于它本身的数有-1，0和1．
其中真命题有（ ）
（2）平方根等于它本身的数有1和0；
（3）倒数等于它本身的数有±1，0；
（4）立方根等于它本身的数有-1，0和1．
其中真命题有（ ）
| A、0个 | B、1个 | C、2个 | D、3个 |
已知菱形的边长为6，一个内角为60°，则此菱形较长的对角线长是（ ）
A、6
| ||
| B、12 | ||
C、3
| ||
| D、6 |
如图，在正八边形ABCDEFGH中，等腰梯形CDEF的面积是12，则这个八边形的面积为（ ）| A、36 | ||
| B、48 | ||
C、24+12
| ||
D、36+6
|
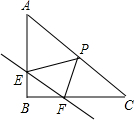已知Rt△ABC，∠B=90°，直线EF分别于两直角边AB、AC交于E、F两点，且EF∥AC．P是斜边AC的中点，连接PE、PF，且已知AB=