题目内容
14.设方程x2+ax+b=0与x2+bx+a=0(a<0,b<0,a≠b)有一个公共根,设它们另两个根分别为x1,x2,求x1+x2的值.分析 设出公共根x0构造二元一次方程组,解出符合条件的公共根,进一步代入求得答案即可.
解答 解:设x0是方程的公共根,则$\left\{\begin{array}{l}{x_0}^2+a{x_0}+b=0\\{x_0}^2+b{x_0}+a=0\end{array}\right.$,相减得(a-b)x0+(b-a)=0
得x0=1,且1+a+b=0
同时$\left\{\begin{array}{l}{x_1}+1=-a\\{x_2}+1=-b\end{array}\right.$,则x1+x2=-a-b-2=-1
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.

练习册系列答案
相关题目
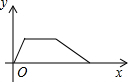
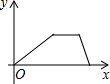
4. 某单位3月上旬中的1至6日每天用水量的变化如图所示,那么这6天用水量的中位数是( )
某单位3月上旬中的1至6日每天用水量的变化如图所示,那么这6天用水量的中位数是( )
 某单位3月上旬中的1至6日每天用水量的变化如图所示,那么这6天用水量的中位数是( )
某单位3月上旬中的1至6日每天用水量的变化如图所示,那么这6天用水量的中位数是( )| A. | 31.5 | B. | 32 | C. | 32.5 | D. | 33 |
5.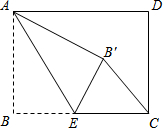 矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为( )
矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为( )
 矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为( )
矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为( )| A. | 3 | B. | $\frac{3}{2}$ | C. | 2或3 | D. | 3或$\frac{3}{2}$ |
19.若三角形的三边长分别为3,4,x,则x的值可能是( )
| A. | 1 | B. | 6 | C. | 7 | D. | 10 |
4.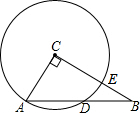 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )
 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )| A. | $\frac{18}{5}$ | B. | $\frac{5}{2}$ | C. | $\frac{24}{5}$ | D. | $\frac{9}{5}$ |
 将直角梯形ABCD平移得梯形EFGH,若HG=10,MC=2,MG=4,则图中阴影部分的面积为36.
将直角梯形ABCD平移得梯形EFGH,若HG=10,MC=2,MG=4,则图中阴影部分的面积为36.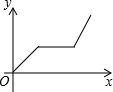
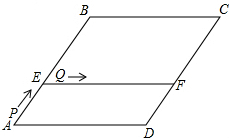 如图,在菱形ABCD中,AB=10,sinA=$\frac{4}{5}$,点E在AB上,AE=4,过点E作EF∥AD,交CD于点F.
如图,在菱形ABCD中,AB=10,sinA=$\frac{4}{5}$,点E在AB上,AE=4,过点E作EF∥AD,交CD于点F.