题目内容
1.若关于x的一元二次方程x2-2x+kb+1=0有两个不相等的实数根,则一次函数y=kx+b的大致图象可能是( )| A. | 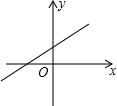 | B. | 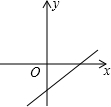 | C. | 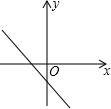 | D. | 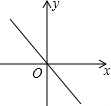 |
分析 根据一元二次方程x2-2x+kb+1=0有两个不相等的实数根,得到判别式大于0,求出kb的符号,对各个图象进行判断即可.
解答 解:∵x2-2x+kb+1=0有两个不相等的实数根,
∴△=4-4(kb+1)>0,
解得kb<0,
A.k>0,b>0,即kb>0,故A不正确;
B.k>0,b<0,即kb<0,故B正确;
C.k<0,b<0,即kb>0,故C不正确;
D.k<0,b=0,即kb=0,故D不正确;
故选:B.
点评 本题考查的是一元二次方程根的判别式和一次函数的图象,一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
12.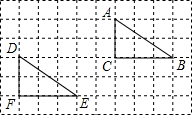 如图,在10×6的网格中,每个小方格的边长都是1个单位,将△DEF平移到△ABC的位置,下列平移方法正确的是( )
如图,在10×6的网格中,每个小方格的边长都是1个单位,将△DEF平移到△ABC的位置,下列平移方法正确的是( )
 如图,在10×6的网格中,每个小方格的边长都是1个单位,将△DEF平移到△ABC的位置,下列平移方法正确的是( )
如图,在10×6的网格中,每个小方格的边长都是1个单位,将△DEF平移到△ABC的位置,下列平移方法正确的是( )| A. | 先向左平移5个单位,再向下平移2个单位 | |
| B. | 先向右平移5个单位,再向下平移2个单位 | |
| C. | 先向左平移5个单位,再向上平移2个单位 | |
| D. | 先向右平移5个单位,再向上平移2个单位 |
6. 如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2015次操作后得到的折痕D2014E2014到BC的距离记为h2015.若h1=1,则h2015的值为( )
如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2015次操作后得到的折痕D2014E2014到BC的距离记为h2015.若h1=1,则h2015的值为( )
 如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2015次操作后得到的折痕D2014E2014到BC的距离记为h2015.若h1=1,则h2015的值为( )
如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2015次操作后得到的折痕D2014E2014到BC的距离记为h2015.若h1=1,则h2015的值为( )| A. | $\frac{1}{{2}^{2015}}$ | B. | $\frac{1}{{2}^{2014}}$ | C. | 1-$\frac{1}{{2}^{2015}}$ | D. | 2-$\frac{1}{{2}^{2014}}$ |
13.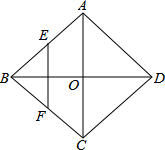 如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF.若EF=$\sqrt{3}$,BD=4,则菱形ABCD的周长为( )
如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF.若EF=$\sqrt{3}$,BD=4,则菱形ABCD的周长为( )
 如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF.若EF=$\sqrt{3}$,BD=4,则菱形ABCD的周长为( )
如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF.若EF=$\sqrt{3}$,BD=4,则菱形ABCD的周长为( )| A. | 4 | B. | 4$\sqrt{6}$ | C. | 4$\sqrt{7}$ | D. | 28 |
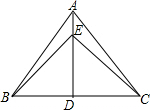 如图,AD是△ABC的高.在AD上取点E,使DE=BD,CE=AB,连接BE
如图,AD是△ABC的高.在AD上取点E,使DE=BD,CE=AB,连接BE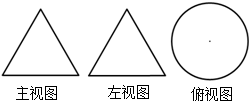 如图是某个几何体的三视图,该几何体是圆锥.
如图是某个几何体的三视图,该几何体是圆锥. 如图,直线l1、l2、…l6是一组等距的平行线,过直线l1上的点A作两条射线,分别与直线l3、l6相交于点B、E、C、F.若BC=2,则EF的长是5.
如图,直线l1、l2、…l6是一组等距的平行线,过直线l1上的点A作两条射线,分别与直线l3、l6相交于点B、E、C、F.若BC=2,则EF的长是5. 如图,∠2=40°,∠3=100°,∠4=80°,求∠1的度数.
如图,∠2=40°,∠3=100°,∠4=80°,求∠1的度数.