题目内容
19.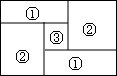 如图,原有一大长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若原来该大长方形的周长是120,则分割后不用测量就能知道周长的图形标号为( )
如图,原有一大长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若原来该大长方形的周长是120,则分割后不用测量就能知道周长的图形标号为( )| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
分析 首先设图形①的长和宽分别是a、c,图形②的边长是b,图形③的边长是d,由于原来该大长方形的周长是120,得出2(a+2b+c)=120,a=b+d,b=c+d;然后分别判断出图形①、图形②的周长都等于原来大长方形的周长的$\frac{1}{2}$,所以它们的周长不用测量就能知道,而图形③的周长不用测量无法知道,据此解答即可.
解答  解:如图,设图形①的长和宽分别是a、c,图形②的边长是b,图形③的边长是d,
解:如图,设图形①的长和宽分别是a、c,图形②的边长是b,图形③的边长是d,
∵原来该大长方形的周长是120,
∴2(a+2b+c)=120.
根据图示,可得$\left\{\begin{array}{l}{a=b+d①}\\{b=c+d②}\end{array}\right.$,
①-②,可得:a-b=b-c,
∴2b=a+c,
∴120=2(a+2b+c)=2×2(a+c)=4(a+c),或120=2(a+2b+c)=2×4b=8b,
∴2(a+c)=60,4b=60,
∵图形①的周长是2(a+c),图形②的周长是4b,
∴图形①②的周长是定值,不用测量就能知道,图形③的周长不用测量无法知道.
∴分割后不用测量就能知道周长的图形的标号为①②.
故选:A.
点评 此题主要考查了中心对称图形的性质和应用,要熟练掌握,解答此题的关键是要明确中心对称的性质:①关于中心对称的两个图形能够完全重合;②关于中心对称的两个图形,对应点的连线都经过对称中心,并且被对称中心平分.

练习册系列答案
相关题目
9.下列运算正确的是( )
| A. | -3-2=-1 | B. | -32=8 | C. | 2xy+xy=3xy | D. | 2x+x2=3x3 |
10.已知等腰三角形的一边长为4,另一边长为8,则它的周长是( )
| A. | 12 | B. | 16 | C. | 16或20 | D. | 20 |
7. 古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16 …这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以 看作两个相邻“三角形数”之和下列等式中符合这一规律的是( )
古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16 …这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以 看作两个相邻“三角形数”之和下列等式中符合这一规律的是( )
 古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16 …这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以 看作两个相邻“三角形数”之和下列等式中符合这一规律的是( )
古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16 …这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以 看作两个相邻“三角形数”之和下列等式中符合这一规律的是( )| A. | 13=3+10 | B. | 25=9+16 | C. | 36=14+22 | D. | 49=21+28 |
14.下列计算正确的是( )
| A. | 4x2+2x2=6x4 | B. | (x-y)2=x2-y2 | C. | (x3)2=x5 | D. | x2•x2=x4 |
4.下面计算结果正确的是(( )
| A. | b3•b3=2b3 | B. | x4•x4=x16 | C. | (ab2)3=a3b6 | D. | (-2a)2=-4a2 |
11.中国的陆地面积约为9600000km2,用科学记数法表示9600000为( )
| A. | 96×106 | B. | 9.6×105 | C. | 9.6×106 | D. | 96×105 |