Question

7．胡老师是一名钓鱼爱好者，图乙是他在垂钓（图甲）的示意图，其中钓鱼竿AC的长为6米，露出水面的钓鱼线BC的长为3米，胡老师把钓鱼竿AC往上提竿到AD的位置，使得∠DAC=45°，求前后两次钓鱼线的水平距离BE的长（结果保留根号）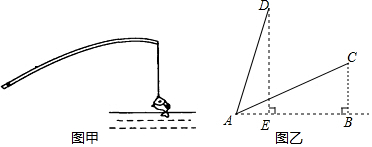

Answer 1

分析 Rt△ABC中由AC=6、BC=3得AB=3$\sqrt{2}$、∠BAC=30°，从而知∠DAE=75°、∠D=15°，作AD的垂直平分线交AD于点F，交DE于点G，可得∠AGE=30°，设AE=x、AG=DG=2x，知GE=$\sqrt{3}$x、DE=（2+$\sqrt{3}$）x，Rt△ADE中，由AE²+DE²=AD²可得x的值，继而可得答案．

解答 解：如图，在Rt△ABC中，
∵AC=6、BC=3，
∴AB=$\sqrt{A{C}^{2}-B{C}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{2}$，∠BAC=30°，
∵∠DAC=45°，
∴∠DAE=75°，∠D=15°，
作AD的垂直平分线交AD于点F，交DE于点G，

则∠D=∠DAG=15°，DG=AG，
∴∠AGE=30°，
设AE=x，则AG=DG=2x，
∴GE=AGcos∠AGE=2x•$\frac{\sqrt{3}}{2}$=$\sqrt{3}$x，
∴DE=DG+EG=2x+$\sqrt{3}$x=（2+$\sqrt{3}$）x，
在Rt△ADE中，由AE²+DE²=AD²可得x²+[（2+$\sqrt{3}$）x]²=6²，
解得：x=$\frac{3}{2}$（$\sqrt{6}$-$\sqrt{2}$）或x=-$\frac{3}{2}$（$\sqrt{6}$-$\sqrt{2}$）（舍），
即AE=$\frac{3}{2}$（$\sqrt{6}$-$\sqrt{2}$），
∴BE=AB-AE=3$\sqrt{3}$-$\frac{3}{2}$（$\sqrt{6}$-$\sqrt{2}$）=$\frac{6\sqrt{3}-3\sqrt{6}+3\sqrt{2}}{2}$．

点评 本题主要考查解直角三角形的应用，通过作中垂线将15度角转化为30度的特殊角求解是解题的关键．