题目内容
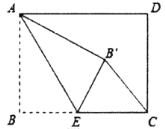
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,把
,把![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处,当
处,当![]() 为直角三角形时,
为直角三角形时,![]() 的长为( )
的长为( )
A. 3B. ![]() C. 2或3D. 3或
C. 2或3D. 3或![]()
【答案】D
【解析】
当△CEB′为直角三角形时,有两种情况:①当点B′落在矩形内部时,如答图1所示.连结AC,先利用勾股定理计算出AC=5,根据折叠的性质得∠AB′E=∠B=90°,而当△CEB′为直角三角形时,只能得到∠EB′C=90°,所以点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,则EB=EB′,AB=AB′=3,可计算出CB′=2,设BE=x,则EB′=x,CE=4-x,然后在Rt△CEB′中运用勾股定理可计算出x.
②当点B′落在AD边上时,如答图2所示.此时ABEB′为正方形.
当△CEB′为直角三角形时,有两种情况:
①当点B′落在矩形内部时,如答图1所示。
连结AC,
在Rt△ABC中,AB=3,BC=4,
∴AC=![]()
∵∠B沿AE折叠,使点B落在点B′处,
∴∠AB′E=∠B=90°,
当△CEB′为直角三角形时,只能得到∠EB′C=90°,
∴点A. B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,
∴EB=EB′,AB=AB′=3,
∴CB′=53=2,
设BE=x,则EB′=x,CE=4x,
在Rt△CEB′中,
∵EB′2+CB′2=CE2,
∴x2+22=(4x)2,解得x=![]() ,
,
∴BE=![]() ;
;
②当点B′落在AD边上时,如答图2所示。
此时ABEB′为正方形,
∴BE=AB=3.
综上所述,BE的长为![]() 或3.
或3.
故选:D.


【题目】将一些数排列成下表中的四列:
第1列 | 第2列 | 第3列 | 第4列 | |
第1行 | 1 | 4 | 5 | 10 |
第2行 | 4 | 8 | 10 | 12 |
第3行 | 9 | 12 | 15 | 14 |
… | … | … | … | … |
(1)第4行第1列的数是多少?直接写出答案;
(2)第17行的四个数之和是多少?请写出适当的过程;
(3)数100所在的行和列分别是多少?直接写出答案.
【题目】下表是某网约车公司的专车计价规则.
计费项目 | 起租价 | 里程费 | 时长费 | 远途费 |
单价 | 15元 | 2.5元/公里 | 1.5元/分 | 1元/公里 |
注:车费由起租价、里程费、时长费、远途费四部分构成,其中起租价15元含10分钟时长费和5公里里程费,远途费的收取方式为:行车里程10公里以内(含10公里)不收远途费,超过10公里的,超出部分每公里收1元.
(1)若小李乘坐专车,行车里程为20公里,行车时间为30分,则需付车费_______元.
(2)若小李乘坐专车,行车里程为![]() 公里,平均时速为
公里,平均时速为![]() ,则小李应付车费多少元? (用含
,则小李应付车费多少元? (用含![]() 的代数式表示)
的代数式表示)
(3)小李与小王各自乘坐专车,行车车费之和为76元,里程之和为15公里(其中小王的行车里程不超过5公里).如果行驶时间均为 20分钟,那么这两辆专车此次的行驶路程各为多少公里?