Question

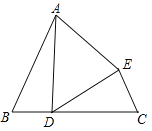
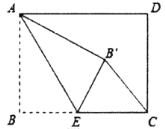
【题目】如图，ABCD为平行四边形，AD＝2，BE∥AC，DE交AC的延长线于F点，交BE于E点.

（1）求证：EF＝DF；

（2）若AC=2CF,∠ADC=60 o, AC⊥DC，求DE的长.

Answer 1

【答案】（1）见解析（2）DE=

【解析】

（1）先过点E作EG∥CD交AF的延长线于点G，由EG∥CD，AB∥CD，可得，AB∥GE，再由BE∥AG，那么四边形ABEG是平行四边形，就可得，AB=GE=CD，而GE∥CD，会出现两对内错角相等，故△EGF≌△DCF，即EF=DF．

（2）有AC⊥DC，∠ADC=60°，可得CD=AD=1，利用勾股定理，可求AC=，而CF=AC，那么再利用勾股定理，又可求DF，而由（1）知，DE=2DF，故可求．

（1）证明：过点E作EG∥CD交AF的延长线于点G

则∠GEF＝∠CDF，∠G＝∠DCF

在平行四边形ABCD中，AB∥CD，AB＝CD

∴EG∥AB

∵BE∥AC

∴四边形ABEG是平行四边形

∴EG＝AB＝CD

∴△EGF≌△DCF

∴EF＝DF

（2）∵∠ADC=60 o, AC⊥DC

∴∠CAD＝30 o

∵AD＝2

∴CD＝1

∴AC＝

又AC=2CF，

∴CF＝

在Rt△DGF中

DF＝＝

∴DE＝2DF＝