题目内容
不等式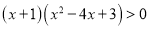
有多种解法，其中有一种方法如下，在同一直角坐标系中做出
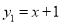和
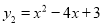的图像然后进行求解，请类比求解以下问题：
设a，b为整数，若对任意x≤0，都有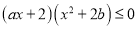
成立，则a＋b＝________．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
新课标同步训练系列答案一线名师口算应用题天天练一本全系列答案题目内容
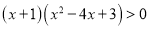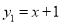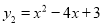不等式有多种解法，其中有一种方法如下，在同一直角坐标系中做出和的图像然后进行求解，请类比求解以下问题：
设a，b为整数，若对任意x≤0，都有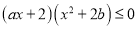成立，则a＋b＝________．
新课标同步训练系列答案一线名师口算应用题天天练一本全系列答案
实数范围内有意义，则x的取值范围是（ ）
成立，则
= 
，则
的解有________个．
．求BE的长．
=______．