题目内容
12. 如图,平面直角坐标系中,矩形OABC的顶点B在第一象限,点C在x轴上,点A在y轴上,D、E分别是AB,OA中点.过点D的双曲线y=$\frac{k}{x}$(x>0,k>0)与BC交于点G.连接DC,F在DC上,且DF:FC=3:1,连接DE,EF.若△DEF的面积为6,则k的值为( )
如图,平面直角坐标系中,矩形OABC的顶点B在第一象限,点C在x轴上,点A在y轴上,D、E分别是AB,OA中点.过点D的双曲线y=$\frac{k}{x}$(x>0,k>0)与BC交于点G.连接DC,F在DC上,且DF:FC=3:1,连接DE,EF.若△DEF的面积为6,则k的值为( )| A. | $\frac{16}{3}$ | B. | $\frac{32}{3}$ | C. | 6 | D. | 10 |
分析 设矩形OABC中OA=2a、AB=2b,由D、E分别是AB,OA中点知点D(b,2a)、E(0,a),过点F作FP⊥BC于点P,延长PF交OA于点Q,可得四边形OCPQ是矩形,即OQ=PC、PQ=OC=2b,证△CFP∽△CDB得$\frac{CP}{CB}$=$\frac{FP}{DB}$=$\frac{CF}{CD}$,可得CP=$\frac{a}{2}$,FP=$\frac{b}{4}$、EQ=EO-OQ=$\frac{a}{2}$、FQ=PQ-PF=$\frac{7b}{4}$,根据S梯形ADFQ-S△ADE-S△EFQ=6求得ab即可得答案.
解答 解:设矩形OABC中OA=2a,AB=2b,
∵D、E分别是AB,OA中点,
∴点D(b,2a)、E(0,a),
如图,过点F作FP⊥BC于点P,延长PF交OA于点Q,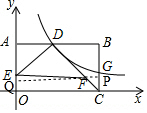
∵四边形OABC是矩形,
∴∠QOC=∠OCP=∠CPQ=90°,
∴四边形OCPQ是矩形,
∴OQ=PC,PQ=OC=2b,
∵FP⊥BC、AB⊥BC,
∴FP∥DB,
∴△CFP∽△CDB,
∴$\frac{CP}{CB}$=$\frac{FP}{DB}$=$\frac{CF}{CD}$,即$\frac{CP}{2a}=\frac{FP}{b}=\frac{1}{4}$,
可得CP=$\frac{a}{2}$,FP=$\frac{b}{4}$,
则EQ=EO-OQ=a-$\frac{a}{2}$=$\frac{a}{2}$,FQ=PQ-PF=2b-$\frac{b}{4}$=$\frac{7b}{4}$,
∵△DEF的面积为6,
∴S梯形ADFQ-S△ADE-S△EFQ=6,
即$\frac{1}{2}$•(b+$\frac{7}{4}$b)•$\frac{3}{2}$a-$\frac{1}{2}$ab-$\frac{1}{2}$×$\frac{7}{4}$b•$\frac{a}{2}$=6,
可得ab=$\frac{16}{3}$,
则k=2ab=$\frac{32}{3}$,
故选:B
点评 本题主要考查反比例函数系数的几何意义及相似三角形的判定与性质、矩形的判定与性质及三角形的面积,利用相似三角形的判定与性质表示出点F的坐标是解题的关键.

 阅读快车系列答案
阅读快车系列答案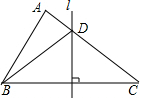 如图,△ABC中,AB+AC=6cm,BC的垂直平分线l与AC相交于点D,则△ABD的周长为( )
如图,△ABC中,AB+AC=6cm,BC的垂直平分线l与AC相交于点D,则△ABD的周长为( )| A. | 12cm | B. | 10cm | C. | 8cm | D. | 6cm |
| A. | 4cm | B. | 5cm | C. | 6cm | D. | 9cm |
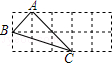 如图,在5×2方格纸中,有一个以格点为顶点的△ABC,请你找出方格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有4个.
如图,在5×2方格纸中,有一个以格点为顶点的△ABC,请你找出方格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有4个.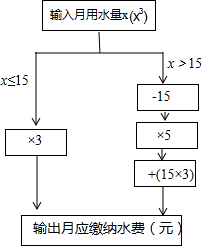 小明根据市自来水公司的居民用水收费标准,制定了如图所示的水费计算数值转换机示意图,根据数值转换机程序,小明输入他家这个月的用水量,结果显示应缴水费70元,那么小明家这个月的用水量为20m3.
小明根据市自来水公司的居民用水收费标准,制定了如图所示的水费计算数值转换机示意图,根据数值转换机程序,小明输入他家这个月的用水量,结果显示应缴水费70元,那么小明家这个月的用水量为20m3.
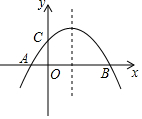 如图,已知抛物线y=-$\frac{1}{m}$(x+2)(x-m)(m>0)与x轴相交于点A、B,与y轴相交于点C,且点A在点B的左侧.
如图,已知抛物线y=-$\frac{1}{m}$(x+2)(x-m)(m>0)与x轴相交于点A、B,与y轴相交于点C,且点A在点B的左侧.