题目内容
三条线段长分别是
、
、
，则此三条线段所构成的三角形是（ ）
| 3 |
| 7 |
| 10 |
| A、锐角三角形 |
| B、钝角三角形 |
| C、一般的不等边三角形 |
| D、直角三角形 |
考点：三角形三边关系,实数大小比较
专题：
分析：根据勾股定理的逆定理即可作出判断．
解答：解：∵（
）2+（
）2=（
）2，
∴三条线段组成的三角形是直角三角形．
故选D．
| 3 |
| 7 |
| 10 |
∴三条线段组成的三角形是直角三角形．
故选D．
点评：本题考查了勾股定理的逆定理：如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形．
练习册系列答案
相关题目
若⊙O1、⊙O2的半径分别为4和6，圆心距O1O2=2，则⊙O1与⊙O2的位置关系是（ ）
| A、相交 | B、内切 | C、外切 | D、外离 |
10名同学分成甲、乙两队进行篮球比赛，他们的身高（单位：cm）如下表所示：
设两队队员身高的平均数依次为
甲，
乙，身高的方差依次为S2甲，S2乙，则下列关系中完全正确的是（ ）
| 队员1 | 队员2 | 队员3 | 队员4 | 队员5 | |
| 甲队 | 173 | 175 | 175 | 175 | 177 |
| 乙队 | 170 | 171 | 175 | 179 | 180 |
. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
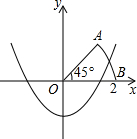如图，以扇形OAB的顶点O为原点，半径OB所在的直线为x轴，建立平面直角坐标系，点B的坐标为（2，0），若抛物线y=x2+k与扇形OAB的边界总有公共点，则实数k的取值范围是（ ）A、
| ||
B、-4≤k≤
| ||
C、C-4≤k≤
| ||
| D、-4≤k≤0 |
如图，在等边三角形ABC中，AB=2，AD平分∠BAC，交BC于点D，DE⊥AB于点E，DF⊥AC于点F，则下列说法错误的是（ ）| A、DE=DF | ||||
| B、∠BDE=∠CDF=30° | ||||
C、AD=
| ||||
D、S△BDE=
|
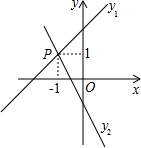如图，已知直线y1=x+m与y2=kx-1相交于点P（-1，1），关于x的不等式x+m＞kx-1的解集是（ ）| A、x≥-1 | B、x＞-1 |
| C、x≤-1 | D、x＜-1 |
若
=
，则
等于（ ）
| x |
| y |
| 2 |
| 7 |
| 7x2-3xy+2y2 |
| 2x2-3xy+7y2 |
A、
| ||
B、
| ||
| C、7 | ||
| D、1 |