题目内容
11.在等腰△ABC中,∠A=4∠B,则∠C的度数为( )| A. | 30° | B. | 60° | C. | 30°或80° | D. | 60°或80° |
分析 根据三角形的内角和定理得∠A+∠B+∠C=180°,而∠A=4∠B=∠C,则有∠B+4∠B+4∠B=180°,或∠A=4∠B=4∠C,则有∠B+4∠B+∠B=180°,解方程即可得到∠C的度数.
解答 解:∵∠A+∠B+∠C=180°,∠A=4∠B,
∴当∠A=∠C时,
即4∠B+4∠B+∠B=180°,
∴∠B=20°,
∴∠C=80°,
当∠B=∠C时,
即∠B+4∠B+∠B=180°,
∴∠B=30°,
∴∠C=30°,
综上所述:∠C的度数为30°或80°.
故选C.
点评 本题考查了等腰三角形的性质,三角形的内角和定理,熟练掌握等腰三角形的性质是解题的关键.

练习册系列答案
相关题目
2.在锐角的内部引射线,当n=1,n=2时,图中小于180°角的个数及规律如表,请你在表中空白处填出射线为3和n的情形.
| 图形 |  | 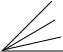 | 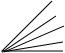 | 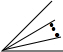 |
| n | 1 | 2 | 3 | n |
| 个数及规律 | 3=1+2=$\frac{2×3}{2}$ | 6=1+2+3=$\frac{3×4}{2}$ | 10=1+2+3+4=$\frac{4×5}{2}$ | 1+2+3+…+n+1=$\frac{(n+1)(n+2)}{2}$. |
 如图,一块矩形的土地,长48m,宽24m,要在它的中央划一块矩形的草地,四周铺上花砖路,路面宽都相等,草地占去矩形土地的$\frac{5}{9}$,则花砖路面的宽为多少?
如图,一块矩形的土地,长48m,宽24m,要在它的中央划一块矩形的草地,四周铺上花砖路,路面宽都相等,草地占去矩形土地的$\frac{5}{9}$,则花砖路面的宽为多少?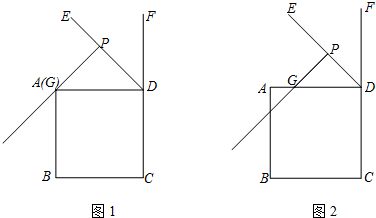
 如图,点A、B、C、D、E、F为⊙O的六等分点,动点P从圆心O出发,沿OE弧EFFO的路线做匀速运动,设运动的时间为t,∠BPD的度数为y,则下列图象中表示y与t之间函数关系最恰当的是( )
如图,点A、B、C、D、E、F为⊙O的六等分点,动点P从圆心O出发,沿OE弧EFFO的路线做匀速运动,设运动的时间为t,∠BPD的度数为y,则下列图象中表示y与t之间函数关系最恰当的是( )



 如图,BD是△ABC的角平分线,DE⊥AB于点E.△ABC的面积为20,AB=12,BC=8,则DE的长为2.
如图,BD是△ABC的角平分线,DE⊥AB于点E.△ABC的面积为20,AB=12,BC=8,则DE的长为2.