题目内容
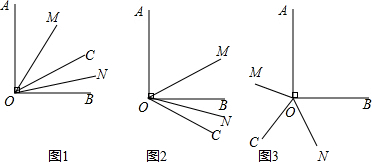
6. 如图,点A、B、C、D、E、F为⊙O的六等分点,动点P从圆心O出发,沿OE弧EFFO的路线做匀速运动,设运动的时间为t,∠BPD的度数为y,则下列图象中表示y与t之间函数关系最恰当的是( )
如图,点A、B、C、D、E、F为⊙O的六等分点,动点P从圆心O出发,沿OE弧EFFO的路线做匀速运动,设运动的时间为t,∠BPD的度数为y,则下列图象中表示y与t之间函数关系最恰当的是( )| A. |  | B. |  | C. |  | D. |  |
分析 利用点A、B、C、D、E、F为⊙O的六等分点可得到∠BOC=∠COD=60°,所以P在O点时,∠BPD=120°,P在弧EF上时,∠BPD=$\frac{1}{2}$∠BOD=60°,然后分类讨论:当点P从O点运动到E点时,易得y由120°逐渐减小到60°;当点P在弧EF上运动时,y=60°;当点P从F点运动到O点时,易得y由60°逐渐增大到120°,根据此特征可对四个选项进行判断.
解答 解:因为点A、B、C、D、E、F为⊙O的六等分点,
所以∠BOC=∠COD=60°,
当P在O点时,∠BPD=120°,当P在弧EF上时,∠BPD=$\frac{1}{2}$∠BOD=60°,
当点P从O点运动到E点时,y由120°逐渐减小到60°;当点P在弧EF上运动时,y的值不变,为60°;当点P从F点运动到O点时,y由60°逐渐增大到120°.
故选C.
点评 本题考查了动点问题的函数图象:函数图象是典型的数形结合,图象应用信息广泛,通过看图获取信息,不仅可以解决生活中的实际问题,还可以提高分析问题、解决问题的能力.解决本题的关键是圆周角定理的应用.

练习册系列答案
相关题目
14.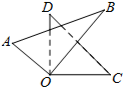 如图是由一副三角尺拼成的图案,它们有公共顶点O,且有一部分重叠,已知∠BOD=40°,则∠AOC的度数是( )
如图是由一副三角尺拼成的图案,它们有公共顶点O,且有一部分重叠,已知∠BOD=40°,则∠AOC的度数是( )
 如图是由一副三角尺拼成的图案,它们有公共顶点O,且有一部分重叠,已知∠BOD=40°,则∠AOC的度数是( )
如图是由一副三角尺拼成的图案,它们有公共顶点O,且有一部分重叠,已知∠BOD=40°,则∠AOC的度数是( )| A. | 40° | B. | 120° | C. | 140° | D. | 150° |
11.在等腰△ABC中,∠A=4∠B,则∠C的度数为( )
| A. | 30° | B. | 60° | C. | 30°或80° | D. | 60°或80° |
18.数据50,20,50,30,25,50,55的众数和中位数分别是( )
| A. | 50,30 | B. | 50,40 | C. | 50,50 | D. | 50,55 |
15.化简|-2|,-(-2)2,-(-2),(-2)3这四个数中,负数的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图所示,在平面直角坐标系中,点A、B的坐标分别为(4,2)和(3,0),将△OAB绕原点O按逆时针方向旋转90°得到△OA′B′.
如图所示,在平面直角坐标系中,点A、B的坐标分别为(4,2)和(3,0),将△OAB绕原点O按逆时针方向旋转90°得到△OA′B′.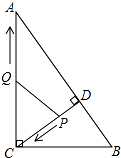 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.