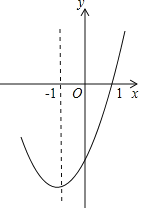ƒøƒ⁄»ð
°æƒø°ø»ÁÕº£¨Àƒ±þ–Œ![]() Œ™÷±Ω«Ã𖌣¨
Œ™÷±Ω«Ã𖌣¨![]() £¨
£¨![]() £¨
£¨![]() £Æµ„
£Æµ„![]() ¥”
¥”![]() ≥ˆ∑¢“‘√ø√Î2∏ˆµ•Œª≥§∂»µƒÀŸ∂»œÚ
≥ˆ∑¢“‘√ø√Î2∏ˆµ•Œª≥§∂»µƒÀŸ∂»œÚ![]() ‘À∂Ø£ªµ„
‘À∂Ø£ªµ„![]() ¥”
¥”![]() Õ¨ ±≥ˆ∑¢£¨“‘√ø√Î1∏ˆµ•Œª≥§∂»µƒÀŸ∂»œÚ
Õ¨ ±≥ˆ∑¢£¨“‘√ø√Î1∏ˆµ•Œª≥§∂»µƒÀŸ∂»œÚ![]() ‘À∂Ø£Æ∆‰÷–“ª∏ˆ∂ص„µΩ¥Ô÷’µ„ ±£¨¡Ì“ª∏ˆ∂ص„“≤ÀÊ÷ÆÕ£÷π‘À∂Ø£Æπ˝µ„
‘À∂Ø£Æ∆‰÷–“ª∏ˆ∂ص„µΩ¥Ô÷’µ„ ±£¨¡Ì“ª∏ˆ∂ص„“≤ÀÊ÷ÆÕ£÷π‘À∂Ø£Æπ˝µ„![]() ◊˜
◊˜![]() ¥π÷±
¥π÷±![]() ÷·”⁄µ„
÷·”⁄µ„![]() £¨¡¨Ω”
£¨¡¨Ω”![]() Ωª
Ωª![]() ”⁄
”⁄![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £Æ
£Æ
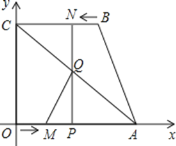
(1) «Û![]() µƒ√ʪ˝
µƒ√ʪ˝![]() ”ΑÀ∂Ø ±º‰
”ΑÀ∂Ø ±º‰![]() µƒ∫Ø ˝πÿœµ Ω£¨ ≤¢–¥≥ˆ◊‘±‰¡ø
µƒ∫Ø ˝πÿœµ Ω£¨ ≤¢–¥≥ˆ◊‘±‰¡ø![]() µƒ»°÷µ∑∂Œß£¨ µ±
µƒ»°÷µ∑∂Œß£¨ µ±![]() Œ™∫Œ÷µ ±£¨
Œ™∫Œ÷µ ±£¨![]() µƒ÷µ◊Ó¥Û£ø
µƒ÷µ◊Ó¥Û£ø
(2) «∑ҥʑ⁄µ„![]() £¨ πµ√
£¨ πµ√![]() Œ™÷±Ω«»˝Ω«–Œ?»Ù¥Ê‘⁄£¨«Û≥ˆµ„
Œ™÷±Ω«»˝Ω«–Œ?»Ù¥Ê‘⁄£¨«Û≥ˆµ„![]() µƒ◊¯±Í£¨»Ù≤ª¥Ê‘⁄£¨Àµ√˜¿Ì”…£Æ
µƒ◊¯±Í£¨»Ù≤ª¥Ê‘⁄£¨Àµ√˜¿Ì”…£Æ
(3) µ±![]() Œ™“‘
Œ™“‘![]() Œ™µ◊µƒµ»—¸»˝Ω«–Œ ±£¨«Û
Œ™µ◊µƒµ»—¸»˝Ω«–Œ ±£¨«Û![]() ÷µ£Æ
÷µ£Æ
(4) «∑ҥʑ⁄’‚—˘µƒ![]() ÷µ£¨ π÷±œþ
÷µ£¨ π÷±œþ![]() Ω´
Ω´![]() µƒ÷Ð≥§∫Õ√ʪ˝Õ¨ ±∆Ω∑÷?»Ù¥Ê‘⁄£¨«Û≥ˆ
µƒ÷Ð≥§∫Õ√ʪ˝Õ¨ ±∆Ω∑÷?»Ù¥Ê‘⁄£¨«Û≥ˆ![]() ÷µ£¨»Ù≤ª¥Ê‘⁄£¨Àµ√˜¿Ì”…£Æ
÷µ£¨»Ù≤ª¥Ê‘⁄£¨Àµ√˜¿Ì”…£Æ
°æ¥∞∏°ø£®1£©![]() £¨µ±
£¨µ±![]() ±£¨”–
±£¨”–![]() £ª£®2£©
£ª£®2£©![]() ªÚ
ªÚ![]() £ª£®3£©
£ª£®3£©![]() £ª£®4£©¥Ê‘⁄£¨µ±
£ª£®4£©¥Ê‘⁄£¨µ±![]() ±£¨÷±œþ
±£¨÷±œþ![]() Ω´
Ω´![]() µƒ÷Ð≥§∫Õ√ʪ˝Õ¨ ±∆Ω∑÷.
µƒ÷Ð≥§∫Õ√ʪ˝Õ¨ ±∆Ω∑÷.
°æΩ‚Œˆ°ø
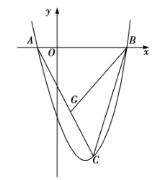
£®1£©π˝µ„B◊˜BD°Õx÷·”⁄D£¨∏˘æðæÿ–Œµƒ–‘÷ ø…µ√BN=PD=t£¨OD=BC=3£¨»ª∫Û∏˘æðµ»—¸÷±Ω«»˝Ω«–Œµƒ–‘÷ ø…µ√![]() ,∏˘æð»˝Ω«–Œ√ʪ˝π´ Ωº¥ø…«Û≥ˆ
,∏˘æð»˝Ω«–Œ√ʪ˝π´ Ωº¥ø…«Û≥ˆ![]() µƒ√ʪ˝
µƒ√ʪ˝![]() ”ΑÀ∂Ø ±º‰
”ΑÀ∂Ø ±º‰![]() µƒ∫Ø ˝πÿœµ Ω£¨»ª∫Û∏˘æ𓂺¥ø…«Û≥ˆtµƒ»°÷µ∑∂Œß£¨‘Ÿ¿˚”√∂˛¥Œ∫Ø ˝«Û◊Ó÷µº¥ø…£ª
µƒ∫Ø ˝πÿœµ Ω£¨»ª∫Û∏˘æ𓂺¥ø…«Û≥ˆtµƒ»°÷µ∑∂Œß£¨‘Ÿ¿˚”√∂˛¥Œ∫Ø ˝«Û◊Ó÷µº¥ø…£ª
£®2£©∏˘æð÷±Ω«µƒ«Èøˆ∑÷¿ýÃ÷¬€£¨∑÷±’“≥ˆµ»¡øπÿœµ¡–≥ˆ∑Ω≥㨺¥ø…«Û≥ˆtµƒ÷µ£ª
£®3£©∑÷±”√∫¨tµƒ Ω◊”±Ì æ≥ˆAQ∫ÕAM£¨»ª∫Û∏˘æðµ»—¸»˝Ω«–Œµƒ∂®“¡–∑Ω≥㨺¥ø…«Û≥ˆtµƒ÷µ£ª
£®4£©∑÷±«Û≥ˆ÷±œþ![]() Ω´
Ω´![]() µƒ÷Ð≥§∆Ω∑÷µƒt÷µ∫Õ÷±œþ
µƒ÷Ð≥§∆Ω∑÷µƒt÷µ∫Õ÷±œþ![]() Ω´
Ω´![]() µƒ√ʪ˝∆Ω∑÷µƒt÷µ£¨»Áπ˚¡Ω∏ˆt÷µœýµ»º¥¥Ê‘⁄£¨≤ªœýµ»º¥≤ª¥Ê‘⁄£Æ
µƒ√ʪ˝∆Ω∑÷µƒt÷µ£¨»Áπ˚¡Ω∏ˆt÷µœýµ»º¥¥Ê‘⁄£¨≤ªœýµ»º¥≤ª¥Ê‘⁄£Æ
Ω‚£∫£®1£©π˝µ„B◊˜BD°Õx÷·”⁄D
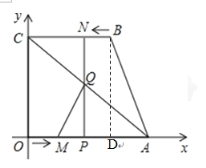
“◊÷™£∫Àƒ±þ–ŒCOPN°¢Àƒ±þ–ŒNPDB∫ÕÀƒ±þ–ŒCODBæ˘Œ™æÿ–Œ
°ýBN=PD=t£¨OD=BC=3
![]()
°ýAD=OA£≠OD=1![]()
![]()
![]()
![]()
µ„M¥”µ„OµΩµ„AÀ˘–Ë ±º‰Œ™£∫OA°¬2=2s£¨µ„N¥”µ„BµΩµ„CÀ˘–Ë ±º‰Œ™£∫BC°¬1=3s£¨
°ý![]()
ªØŒ™∂•µ„ Ω£¨µ√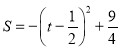 £¨∆‰÷–-1£º0
£¨∆‰÷–-1£º0
°ýµ±![]() ±£¨”–
±£¨”–![]()
£®2£©¢Ÿµ±![]() ±£¨
±£¨
![]()
°ý°˜AQMŒ™µ»—¸÷±Ω«»˝Ω«–Œ
°þQP°ÕAM
°ýQPŒ™°˜AQMµƒ÷–œþ
![]()
![]()
Ω‚µ√£∫![]()
¢⁄![]() ±£¨¥À ±M”ÎP÷ÿ∫œ
±£¨¥À ±M”ÎP÷ÿ∫œ
°ý![]()
![]()
Ω‚µ√![]()
◊€…œ£¨![]() ªÚ
ªÚ![]()
£®3£©°þ![]() Œ™“‘
Œ™“‘![]() Œ™µ◊µƒµ»—¸»˝Ω«–Œ
Œ™µ◊µƒµ»—¸»˝Ω«–Œ
![]()
‘⁄Rt°˜AQP÷–![]()
°þ![]()
°ý![]()
Ω‚µ√£∫![]()
£®4£©√ʪ˝∆Ω∑÷ ±£¨º¥S°˜APQ=![]() S°˜AOC
S°˜AOC
![]()
º¥![]()
Ω‚µ√£∫![]() ªÚ
ªÚ![]() £®≤ª∑˚∫œ µº £¨π …·»•£©
£®≤ª∑˚∫œ µº £¨π …·»•£©
÷Ð≥§∆Ω∑÷ ±£∫![]() £Æ
£Æ
º¥![]()
Ω‚µ√![]()
◊€…œÀ˘ ˆ£∫µ±![]() ±£¨÷±œþ
±£¨÷±œþ![]() Ω´
Ω´![]() µƒ÷Ð≥§∫Õ√ʪ˝Õ¨ ±∆Ω∑÷£Æ
µƒ÷Ð≥§∫Õ√ʪ˝Õ¨ ±∆Ω∑÷£Æ

 » ∞Æ”¢”ÔÕ¨≤Ω¡∑œ∞≤·œµ¡–¥∞∏
» ∞Æ”¢”ÔÕ¨≤Ω¡∑œ∞≤·œµ¡–¥∞∏ —ßœ∞ µº˘‘∞µÿœµ¡–¥∞∏
—ßœ∞ µº˘‘∞µÿœµ¡–¥∞∏°æƒø°ø±Ì÷–À˘¡– ![]() µƒ7∂‘÷µ «∂˛¥Œ∫Ø ˝
µƒ7∂‘÷µ «∂˛¥Œ∫Ø ˝![]() ÕºœÛ…œµƒµ„À˘∂‘”¶µƒ◊¯±Í£¨∆‰÷–
ÕºœÛ…œµƒµ„À˘∂‘”¶µƒ◊¯±Í£¨∆‰÷– ![]()
x | °≠ |
|
|
|
|
|
|
| °≠ |
y | °≠ | 7 | m | 14 | k | 14 | m | 7 | °≠ |
∏˘æð±Ì÷–Ã·π©µƒ–≈œ¢£¨”–“‘œ¬4 ∏ˆ≈–∂œ£∫
¢Ÿ ![]() £ª¢⁄
£ª¢⁄ ![]() £ª¢€ µ±
£ª¢€ µ±![]() ±£¨y µƒ÷µ « k£ª¢Ð
±£¨y µƒ÷µ « k£ª¢Ð ![]() ∆‰÷–≈–∂œ’˝»∑µƒ « £® £©
∆‰÷–≈–∂œ’˝»∑µƒ « £® £©
A. ¢Ÿ¢⁄¢€ B. ¢Ÿ¢⁄¢Ð C. ¢Ÿ¢€¢Ð D. ¢⁄¢€¢Ð