题目内容
观察下列等式,探究其中的规律:①
+
-1=
,②
+
-
=
,③
+
-
=
,④
+
-
=
,….
(1)按以上规律写出第⑧个等式: ;
(2)猜想并写出第n个等式: ;
(3)请证明猜想的正确性.
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 12 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 30 |
| 1 |
| 7 |
| 1 |
| 8 |
| 1 |
| 4 |
| 1 |
| 56 |
(1)按以上规律写出第⑧个等式:
(2)猜想并写出第n个等式:
(3)请证明猜想的正确性.
考点:规律型:数字的变化类,分式的加减法
专题:
分析:(1)由算式看一看出三个分数的分子为1,运算符号为+-,第一个数的分母为连续奇数,第二个数的分母为连续偶数,第三个数的分母为连续自然数,由此写出答案即可;
(2)利用(1)的规律写出第n个等式即可;
(3)利用分式的运算计算验证即可.
(2)利用(1)的规律写出第n个等式即可;
(3)利用分式的运算计算验证即可.
解答:(1)解:
+
-
=
;
(2)解:
+
-
=
;
(3)证明:左边=
=
,
右边=
.
左边=右边,
所以
+
-
=
.
| 1 |
| 15 |
| 1 |
| 16 |
| 1 |
| 8 |
| 1 |
| 240 |
(2)解:
| 1 |
| 2n-1 |
| 1 |
| 2n |
| 1 |
| n |
| 1 |
| 2n(2n-1) |
(3)证明:左边=
| 2n+2n-1-2(2n-1) |
| 2n(2n-1) |
| 1 |
| 2n(2n-1) |
右边=
| 1 |
| 2n(2n-1) |
左边=右边,
所以
| 1 |
| 2n-1 |
| 1 |
| 2n |
| 1 |
| n |
| 1 |
| 2n(2n-1) |
点评:此题考查数字的变化规律,发现规律,利用规律解决问题.

练习册系列答案
相关题目
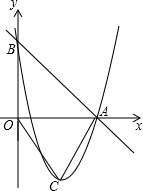 如图,在直角坐标平面内,直线y=-x+5与x轴和y轴分别交于A、B两点,二次函数y=x2+bx+c的图象经过点A、B,且顶点为C.
如图,在直角坐标平面内,直线y=-x+5与x轴和y轴分别交于A、B两点,二次函数y=x2+bx+c的图象经过点A、B,且顶点为C.
 如图,在△ABC中,DE是线段BC的垂直平分线,交BC于E,交AC于D.若AB=3,AC=7,则△ABD的周长是
如图,在△ABC中,DE是线段BC的垂直平分线,交BC于E,交AC于D.若AB=3,AC=7,则△ABD的周长是