题目内容
19. 如图,已知?ABCD的面积是S,依次连接?ABCD各边中点构成第二个平行四边形?EFGH,再依次连接第二个平行四边形各边中点构成第三个平行四边形,…以此类推,则第109个平行四边形的面积为$\frac{1}{{2}^{108}}$S.
如图,已知?ABCD的面积是S,依次连接?ABCD各边中点构成第二个平行四边形?EFGH,再依次连接第二个平行四边形各边中点构成第三个平行四边形,…以此类推,则第109个平行四边形的面积为$\frac{1}{{2}^{108}}$S.
分析 连接EG,HF,相交于点O,有平行四边形的判定方法和平行四边形的性质:被对角线分的两个三角形的面积相等,可得新生成的平行四边形和前一个四边形的面积之间的关系,得出规律,按此规律即可求出第109个平行四边形的面积.
解答 解:连接EG,HF,相交于点O,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵H和F为中点,
∴AH=BF,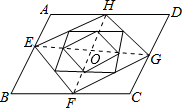
∴四边形ABFH为平行四边形,
∴AE∥HO,
同理可证:EO∥AH,
∴四边形AEOH是平行四边形,
∵EH是对角线,
∴S△AEH=S△EOH=$\frac{1}{2}$SAEOH,
同理可得:S△EOF=S△BEF=$\frac{1}{2}$S四边形EBFO,S△CFG=S△FOG=$\frac{1}{2}$S四边形FOGC,S△DHG=S△HOG=$\frac{1}{2}$S四边形HOGD,
∴S四边形EFGH=$\frac{1}{2}$S四边形ABCD=$\frac{1}{2}$S,
∴第三个平行四边形的面积为$\frac{1}{2}$×$\frac{1}{2}$S,
以此类推,可知每一个新生成的平行四边形都为前一个平行四边形面积的$\frac{1}{2}$,
∴第109个平行四边形的面积=$\frac{1}{{2}^{108}}$S.
故答案为$\frac{1}{{2}^{108}}$S.
点评 本题考查了平行四边形的判定和平行四边形的性质,解题的关键是找到规律,根据规律求出第109个平行四边形的面积.

练习册系列答案
相关题目
10.用加减法解方程组$\left\{\begin{array}{l}{3x-2y=3①}\\{4x+y=15②}\end{array}\right.$时,如果消去y,最简捷的方法是( )
| A. | ①×4-②×3 | B. | ①×4+②×3 | C. | ②×2-① | D. | ②×2+① |
7.方程2x-y=0,5x+3xy=2,3x-y-2x=$\frac{1}{4}$,x2+2x-1=0,$\frac{3}{x}$-2y=5,3x=2y中,二元一次方程的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.下列命题中,真命题的个数有( )
①如果直线a∥b,b∥c,那么a∥c;②相等的角是对顶角;③两条直线被第三条直线所截,同位角相等;④比正实数小的一定是负实数;⑤两条直线平行,同旁内角相等;⑥立方根等于它本身的数是-1,0,1.
①如果直线a∥b,b∥c,那么a∥c;②相等的角是对顶角;③两条直线被第三条直线所截,同位角相等;④比正实数小的一定是负实数;⑤两条直线平行,同旁内角相等;⑥立方根等于它本身的数是-1,0,1.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.龙华轻轨将于2017年6月底投入使用,拟在轨道沿途种植花木共20000棵,为尽量减少施工队交通所造成的影响,实际施工时每天的工效比原计划提高25%,结果提前5天完成种植任务,设原计划每天种植花木x棵,根据题意可列方程为( )
| A. | $\frac{2000}{x}$-$\frac{20000}{x(1-25%)}$=5 | B. | $\frac{20000}{x(1+25%)}$-$\frac{20000}{x}$=5 | ||
| C. | $\frac{20000}{x(1-25%)}$-$\frac{20000}{x}$=5 | D. | $\frac{20000}{x}$-$\frac{2000}{x(1+25%)}$=5 |
11.下列命题中是真命题的是( )
| A. | 对顶角相等 | B. | 内错角相等 | C. | 同旁内角互补 | D. | 同位角相等 |
9.如图,一个长方形是另一个长方形按顺时针方向旋转90°后形成的是( )


| A. | ①② | B. | ②④ | C. | ②③ | D. | ③④ |