题目内容
15.用简便方法计算(1)1-2+3-4+5-6+…+99-100.
(2)$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$…+$\frac{1}{2015×2016}$.
分析 (1)应用加法结合律,求出算式的值是多少即可.
(2)首先把每个分数分成两个分数的差的形式,然后应用加法结合律,求出算式的值是多少即可.
解答 解:(1)1-2+3-4+5-6+…+99-100
=(1-2)+(3-4)+(5-6)+…+(99-100)
=(-1)+(-1)+(-1)+…+(-1)
=-50
(2)$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$…+$\frac{1}{2015×2016}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2015}$-$\frac{1}{2016}$
=1-$\frac{1}{2016}$
=$\frac{2015}{2016}$
点评 此题主要考查了有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
5. 如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
 如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )| A. | △ABC 的三条中线的交点 | B. | △ABC 三边的垂直平分线的交点 | ||
| C. | △ABC 三条角平分线的交点 | D. | △ABC 三条高所在直线的交点 |
3.已知点A(-2,y1)、B(-1,y2)、C(3,y3) 都在反比例函数y=$\frac{4}{x}$的图象上,则y1,y2,y3的大小关系是( )
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y3<y1<y2 | D. | y2<y1<y3 |
7.下列各数中,介于3和4之间的数是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{17}$ | C. | $\sqrt{12}$ | D. | $\root{3}{25}$ |
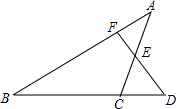 如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,∠A=35°,∠D=50°,求∠ACD的度数.
如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,∠A=35°,∠D=50°,求∠ACD的度数.