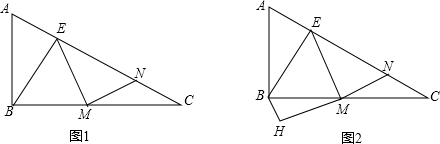
题目内容
18.如图,等边△ABC的边长为4cm,动点D从点B出发,沿射线BC方向移动,以AD为边作等边△ADE.(1)如图①,在点D从点B开始移动至点C的过程中,
①△ADE的面积是否存在最大值或最小值?若存在,直接写出这个最大值或最小值;若不存在,说明理由;
②求点E移动的路径长.
(2)如图②,当点D经过点C,并在继续移动的过程中,点E能否移动至直线AB上?为什么?
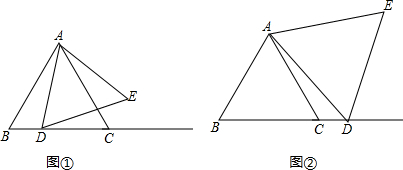
分析 (1)①当AD=AB时,△ADE的面积最大,得出此时面积的值即可;当AD为△ABC的高时,△ADE的面积最小,得出此时面积的值即可;
②连接CE,得出点E的移动距离为CE,利用全等三角形的判定和性质解答即可;
(2)连接CE,利用等边三角形的性质和全等三角形的判定和性质得出点E不能移动至直线AB上.
解答 解:(1)①当AD=AB时,△ADE的面积最大,面积为$\frac{1}{2}×4×2\sqrt{3}=4\sqrt{3}$cm2;
当AD为△ABC的高时,△ADE的面积最小,面积为:$\frac{1}{2}×2\sqrt{3}×3=3\sqrt{3}c{m}^{2}$;
②如图①,连接CE,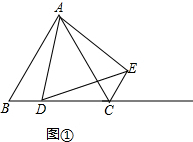
∵△ABC与△ADE都是等边三角形,
∴∠BAC=∠DAE=60°,
∴∠BAC-∠CAD=∠DAE-∠CAD,
即∠BAD=∠CAE,
在△BAD与△CAE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△BAD≌△CAE(SAS),
∴∠ACE=∠B=60°,
∴CE∥AB,即点E在经过点C且与AB平行的直线上移动,
当点D从点B出发时,此时点E与点C重合,
∴点E移动的起点为点C,
当点D到点C停止移动时,此时有AD=AC,
∴在△ACE中,有AC=AE,∠ACE=60°,
∴△ACE是等边三角形,
∴CE=AC=4cm,即点E移动的路径长为4cm;
(2)点E不能移动至直线AB上,
如图②,连接CE,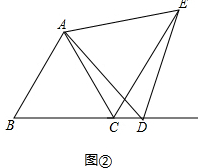
∵△ABC与△ADE都是等边三角形,
∴∠BAC=∠DAE=60°,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠CAE,
在△BAD与△CAE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△BAD≌△CAE(SAS),
∴∠ACE=∠B=60°,
∴CE∥AB,即点E在经过点C且与AB平行的直线上移动,
∴点E不能移动至直线AB上.
点评 此题考查几何变换问题,关键是根据等边三角形的性质和全等三角形的判定和性质进行分析.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案| A. | x≤3 | B. | x≥3 | C. | x≠3 | D. | x=3 |
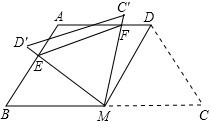 如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是BC的中点.将△MDC绕点M旋转,旋转后对应的三角形为△MC′D′,当MD(即MD′)与AB交于一点E,MC(即MC′)同时与AD交于一点F时,连接EF,求证:EF∥C′D′.
如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是BC的中点.将△MDC绕点M旋转,旋转后对应的三角形为△MC′D′,当MD(即MD′)与AB交于一点E,MC(即MC′)同时与AD交于一点F时,连接EF,求证:EF∥C′D′.
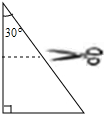 如图所示,是一张直角三角形纸片,其中有一个内角为30°,最小边长为2,点D、E分别是一条直角边和斜边的中点,先将纸片沿DE剪开,然后再将两部分拼成一个四边形,则所得四边形的周长是8或4+2$\sqrt{3}$.
如图所示,是一张直角三角形纸片,其中有一个内角为30°,最小边长为2,点D、E分别是一条直角边和斜边的中点,先将纸片沿DE剪开,然后再将两部分拼成一个四边形,则所得四边形的周长是8或4+2$\sqrt{3}$.