题目内容
19.某商场为了吸引顾客,设置了两种促销方式.一种方式是:让顾客通过转转盘获得购物券.规定顾客每购买100元的商品,就能获得一次转转盘的机会,如果转盘停止后,指针正好对准100元、50元、20元的相应区域,那么顾客就可以分别获得100元、50元、20元购物券,凭购物券可以在该商场继续购物;如果指针对准其它区域,那么就不能获得购物券.另一种方式是:不转转盘,顾客每购买100元的商品,可直接获得10元购物券.据统计,一天中共有1000人次选择了转转盘的方式,其中指针落在100元、50元、20元的次数分别为50次、100次、200次.(1)指针落在不获奖区域的概率约是多少?
(2)通过计算说明选择哪种方式更合算?
分析 (1)利用大量实验下的频率即为概率,进而求出即可;
(2)算出转一次转盘得到金额的平均数,与10比较即可.
解答 解:(1)P(不获奖)=$\frac{1000-50-100-200}{1000}$=$\frac{13}{20}$(或65%);
(2)∵转转盘的平均收益为:100×$\frac{50}{1000}$+50×$\frac{100}{1000}$+20×$\frac{200}{1000}$=14>10,
∴转转盘的方式更合算.
点评 此题主要考查了学生对简单几何概型的掌握情况,既避免了单纯依靠公式机械计算的做法,又体现了数学知识在现实生活、甚至娱乐中的运用,体现了数学学科的基础性.易错点是得到转一次转盘得到金额的平均数.

练习册系列答案
相关题目
14.贵阳数博会于2015年5月26日至29日在贵阳国际会议展览中心举行,贵阳副市长刘春成介绍在近两年签约投资额已经超过了1.4×103多亿元.1.4×103这个数可以表示为( )
| A. | 14 | B. | 140 | C. | 1400 | D. | 14000 |
4.下列运算正确的是( )
| A. | 5y2-2y2=3 | B. | x6+x2=x8 | C. | (-a-b)2=a2-2ab+b2 | D. | $\sqrt{27}$-$\sqrt{12}$=$\sqrt{3}$ |
8.使分式$\frac{2}{2x-6}$有意义的x的取值范围是( )
| A. | x≤3 | B. | x≥3 | C. | x≠3 | D. | x=3 |
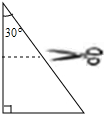 如图所示,是一张直角三角形纸片,其中有一个内角为30°,最小边长为2,点D、E分别是一条直角边和斜边的中点,先将纸片沿DE剪开,然后再将两部分拼成一个四边形,则所得四边形的周长是8或4+2$\sqrt{3}$.
如图所示,是一张直角三角形纸片,其中有一个内角为30°,最小边长为2,点D、E分别是一条直角边和斜边的中点,先将纸片沿DE剪开,然后再将两部分拼成一个四边形,则所得四边形的周长是8或4+2$\sqrt{3}$.
 如果AB∥CF,DE∥CF,∠DCB=40°,∠D=30°,求∠B的度数.
如果AB∥CF,DE∥CF,∠DCB=40°,∠D=30°,求∠B的度数.