Question

4．（1）知识拓展
如图1，由DE∥BC，AD=DB，可得AE=EC；
如2，由AB∥CD∥EF，AE=EC，可得BF=FD；
（2）解决问题
如图3，直线AB与坐标轴分别交于点A（m，0），B（0，n）（m＞0，n＞0），反比例函数y=$\frac{m}{x}$（x＞0）
的图象与AB交于C，D两点．
①若m+n=8，n取何值时△ABO的面积最大？
②若S_△AOC=S_△COD=S_△BOD，求点B的坐标．

Answer 1

分析 ①利用三角形的面积公式得出函数关系式，利用二次函数的极值的确定方法得出最大值；
②借助知识拓展，由S_△AOC=S_△COD=S_△BOD，得出BD=CD=AC，进而得出BF=EF=OE=$\frac{1}{3}$n，再利用点C在反比例函数图象上得出点C坐标，最后利用点C在直线AB上即可求出n即可．

解答 解：①∵m+n=8，∴m=8-n，
∵点A（m，0），B（0，n）（m＞0，n＞0），
∴S_△AOB=$\frac{1}{2}$n（8-n）=-$\frac{1}{2}$（n-4）²+8，
∴当n=4时，△AOB的面积最大，
②如图，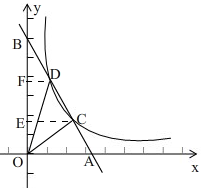

∵S_△AOC=S_△COD=S_△BOD，
∴BD=CD=AC，
过点C作CE⊥OB于E，过点D作DF⊥OB于F，
∴DF∥CE∥OA，
∴BF=EF=OE，
∵点B（0，n）（n＞0），
∴OB=n，
∴BF=EF=OE=$\frac{1}{3}$n，
∴点C的纵坐标为$\frac{1}{3}$n，
∵点C在反比例函数y=$\frac{m}{x}$（x＞0）的图象上，
∴C（$\frac{3m}{n}$，$\frac{1}{3}$n），
∵点A（m，0），B（0，n）（m＞0，n＞0），
∴直线AB的解析式为y=-$\frac{n}{m}$x+n，
∵点C在直线AB上，
∴-$\frac{n}{m}×\frac{3m}{n}+n=\frac{1}{3}n$，
∴n=$\frac{9}{2}$，
∴B（0，$\frac{9}{2}$）．

点评 此题是反比例函数综合题，主要考查了三角形的面积公式，知识拓展得出的结论，待定系数法，解①的关键是建立三角形AOB的面积和n的函数关系式，解②的关键是得出BF=EF=OE=$\frac{1}{3}$n．