题目内容
17．已知图1为图2中三棱柱ABC-EFG的展开图，其中AE，BF，CG，DH是三棱柱的侧棱，若图1中，AD=10，CD=2，求AB长度的取值范围．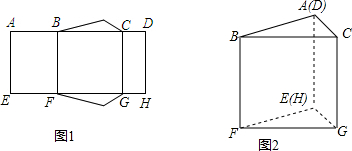
分析 根据图形先求出AB与BC的和，然后设AB=x，表示出BC=8-x，然后利用三角形的任意两边之和大于第三边，两边之差小于第三边列出不等式组，求解得到AB的取值范围，即可得解．
解答 解：由图可知，AD=AB+BC+CD，
∵AD=10，CD=2，
∴AB+BC=8，
设AB=x，则BC=8-x，
所以$\left\{\begin{array}{l}{8-x＜x+2①}\\{8-x＞x-2②}\end{array}\right.$，
解不等式①得x＞3，
解不等式②得，x＜5，
所以，不等式组的解集是3＜x＜5，
∴AB长度的取值范围是3＜x＜5．
点评 本题考查了几何体的展开图，利用三角形的三边关系求出AB边的取值范围是解题的关键．
练习册系列答案
名题训练系列答案
期末集结号系列答案
相关题目
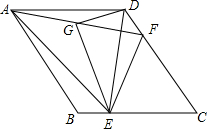如图，在菱形ABCD中，∠ABC=120°，点E、F分别是边BC、CD上一点，且∠DAE=∠BAF，点G是线段AF的中点，连接DG、EG．