题目内容
12.解不等式:(2-$\sqrt{5}$)x<$\sqrt{5}$-2.分析 利用不等式的性质以及二次根式的性质化简求出即可.
解答 解:(2-$\sqrt{5}$)x<$\sqrt{5}$-2
则x>$\frac{\sqrt{5}-2}{2-\sqrt{5}}$,
故x>-1.
点评 此题主要考查了解一元一次不等式以及二次根式的应用,注意2-$\sqrt{5}$的符号是解题关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
1.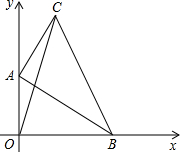 如图,在平面直角坐标系中,Rt△ABC的直角顶点A和顶点B分别在y轴正半轴及x轴正半轴上运动,若AB=4,AC=3,则在运动过程中,线段OC的最大值是( )
如图,在平面直角坐标系中,Rt△ABC的直角顶点A和顶点B分别在y轴正半轴及x轴正半轴上运动,若AB=4,AC=3,则在运动过程中,线段OC的最大值是( )
 如图,在平面直角坐标系中,Rt△ABC的直角顶点A和顶点B分别在y轴正半轴及x轴正半轴上运动,若AB=4,AC=3,则在运动过程中,线段OC的最大值是( )
如图,在平面直角坐标系中,Rt△ABC的直角顶点A和顶点B分别在y轴正半轴及x轴正半轴上运动,若AB=4,AC=3,则在运动过程中,线段OC的最大值是( )| A. | 5 | B. | 2+$\sqrt{13}$ | C. | $\sqrt{13}$ | D. | 6 |
10.下列各式的值最小的是( )
| A. | 0-3 | B. | -22 | C. | -4×0 | D. | |-5| |
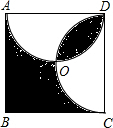 如图,分别以正方形ABCD的边AD和DC为直径画两个半圆交于点O,若正方形的边长为10cm,求阴影部分的面积.
如图,分别以正方形ABCD的边AD和DC为直径画两个半圆交于点O,若正方形的边长为10cm,求阴影部分的面积.