题目内容
5．实数m，n满足|1-n|+（m2+10m+25）=0，则代数式（m-n）2的值为36．分析 首先把m2+10m+25因式分解，进一步利用非负数的性质得出m、n的数值，进一步代入求得答案即可．
解答 解：∵|1-n|+（m2+10m+25）=0，
∴|1-n|+（m+5）2=0，
∴n=1，m=-5，
∴（m-n）2=36．
故答案为：36．
点评 此题考查因式分解的运用，非负数的性质，代数式求值，掌握完全平方公式是解决问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
3．
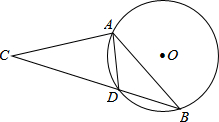如图，在⊙O中，弦AD等于半径，B为优弧AD上的一动点，等腰△ABC的底边BC所在直线经过点D．若⊙O的半径等于1，则OC的长不可能为（ ）
如图，在⊙O中，弦AD等于半径，B为优弧AD上的一动点，等腰△ABC的底边BC所在直线经过点D．若⊙O的半径等于1，则OC的长不可能为（ ）| A． | 2-$\sqrt{3}$ | B． | $\sqrt{3}$-1 | C． | 2 | D． | $\sqrt{3}$+1 |