题目内容
9. 如图所示,点P是边长为4的正方形ABCD的边BC上一点,BP=3.M是BD上一动点,试求MP+MC的最小值.
如图所示,点P是边长为4的正方形ABCD的边BC上一点,BP=3.M是BD上一动点,试求MP+MC的最小值.
分析 由于四边形ABCD是正方形,所以A、C两点关于直线BD对称,连接AP,则AP的长即为MP+MC的最小值,再在Rt△ABP中利用勾股定理即可求出AP的长.
解答  解:∵四边形ABCD是正方形,
解:∵四边形ABCD是正方形,
∴A、C两点关于直线BD对称,
连接AP,则AP的长即为MP+MC的最小值,
在Rt△ABP中,
∵BC=4,BP=3,
∴AP=$\sqrt{A{B}^{2}+B{P}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5.
故MP+MC的最小值是5.
点评 本题考查的是轴对称-最短路线问题及正方形的性质,熟知两点之间线段最短的知识是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.如果两条不同的直线都和第三条直线平行,那么这两条直线的位置关系是( )
| A. | 平行 | B. | 相交 | C. | 平行或相交 | D. | 互相垂直 |
4.在△ABC中,∠A+∠B=120°,∠C=∠A,则△ABC是( )
| A. | 钝角三角形 | B. | 等腰直角三角形 | C. | 直角三角形 | D. | 等边三角形 |
1.一个多边形的各个内角都等于120°,则它的边数为( )
| A. | 3 | B. | 6 | C. | 7 | D. | 8 |
19.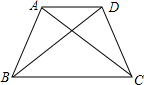 如图,梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,AD=3,BC=5,则梯形ABCD的高是( )
如图,梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,AD=3,BC=5,则梯形ABCD的高是( )
 如图,梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,AD=3,BC=5,则梯形ABCD的高是( )
如图,梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,AD=3,BC=5,则梯形ABCD的高是( )| A. | $4\sqrt{2}$ | B. | 4 | C. | $2\sqrt{2}$ | D. | 2 |
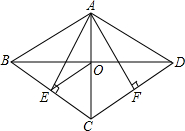 如图 在?ABCD中 对角线AC、BD 相交于点O,AE⊥BC,AF⊥CD,垂足分别是E、F,点E、F恰好为BC、CD的中点,连接OE.
如图 在?ABCD中 对角线AC、BD 相交于点O,AE⊥BC,AF⊥CD,垂足分别是E、F,点E、F恰好为BC、CD的中点,连接OE. 如图,在矩形ABCD中,AB=7cm,BC=$\sqrt{2}$cm,点P从点A出发以1cm/s的速度移动到点B.点P出发$\frac{28-2\sqrt{43}}{3}$秒后,PA=2PC.
如图,在矩形ABCD中,AB=7cm,BC=$\sqrt{2}$cm,点P从点A出发以1cm/s的速度移动到点B.点P出发$\frac{28-2\sqrt{43}}{3}$秒后,PA=2PC.