题目内容
如图所示,在平面直角坐标系中,AB交y轴于点C,连接OB.
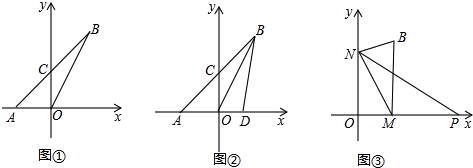
(1)如图①所示,已知A(-2,0),B(2,4),求△AOB的面积;
(2)如图②所示,点D在x轴上,∠OBD=∠OBC,求
的值;
(3)如图③所示,BM⊥x轴于点M,N在y轴上,∠MNB=∠MBN,点P在x轴上,∠MNP=∠MPN,求∠BNP的度数.

(1)如图①所示,已知A(-2,0),B(2,4),求△AOB的面积;
(2)如图②所示,点D在x轴上,∠OBD=∠OBC,求
| ∠BDA-∠BAD |
| ∠BOC |
(3)如图③所示,BM⊥x轴于点M,N在y轴上,∠MNB=∠MBN,点P在x轴上,∠MNP=∠MPN,求∠BNP的度数.
考点:三角形内角和定理,坐标与图形性质,三角形的面积,三角形的外角性质
专题:
分析:(1)根据点A、B的坐标求出OA、点B到OA的距离,然后利用三角形的面积公式列式计算即可得解;
(2)设∠OBD=∠OBC=x,根据点A、B的坐标求出∠BAD=45°,再求出∠ACO=45°,然后根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠BOC,再根据三角形的内角和定理表示出∠BDA,然后代入代数式整理即可得解;
(3)根据点B的坐标求出OM、BM,再求出MN,然后根据直角三角形30°角所对的直角边等于斜边的一半求出∠ONM=30°,再根据直角三角形两锐角互余求出∠OMN=60°,再根据等腰三角形的性质求出∠MNB,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠MNP,然后根据∠BNP=∠MNB-∠MNP计算即可得解.
(2)设∠OBD=∠OBC=x,根据点A、B的坐标求出∠BAD=45°,再求出∠ACO=45°,然后根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠BOC,再根据三角形的内角和定理表示出∠BDA,然后代入代数式整理即可得解;
(3)根据点B的坐标求出OM、BM,再求出MN,然后根据直角三角形30°角所对的直角边等于斜边的一半求出∠ONM=30°,再根据直角三角形两锐角互余求出∠OMN=60°,再根据等腰三角形的性质求出∠MNB,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠MNP,然后根据∠BNP=∠MNB-∠MNP计算即可得解.
解答:解:(1)∵A(-2,0),B(2,4),
∴OA=2,点B到OA的距离是4,
∴△AOB的面积=
×2×4=4;
(2)设∠OBD=∠OBC=x,
∵A(-2,0),B(2,4),
∴∠BAD=45°,
∴∠ACO=45°,
由三角形的外角性质的,∠BOC=∠ACO-∠OBC=45°-x,
由三角形的内角和定理得,∠BDA=180°-∠BAD-∠ABD=180°-45°-2x=135°-2x,
所以,
=
=
=2;
(3)∵BM⊥x轴,点B(2,4),
∴OM=2,BM=4,
∴MN=4,
∴MN=2OM,
∴∠ONM=30°,
∴∠OMN=90°-30°=60°,
∵MN=BM,
∴∠MNB=
(180°-30°)=75°,
∵∠MNP=∠MPN,
∴∠MNP=
∠OMN=
×60°=30°,
∴∠BNP=∠MNB-∠MNP=75°-30°=45°.
∴OA=2,点B到OA的距离是4,
∴△AOB的面积=
| 1 |
| 2 |
(2)设∠OBD=∠OBC=x,
∵A(-2,0),B(2,4),
∴∠BAD=45°,
∴∠ACO=45°,
由三角形的外角性质的,∠BOC=∠ACO-∠OBC=45°-x,
由三角形的内角和定理得,∠BDA=180°-∠BAD-∠ABD=180°-45°-2x=135°-2x,
所以,
| ∠BDA-∠BAD |
| ∠BOC |
| 135°-2x-45° |
| 45°-x |
| 90°-2x |
| 45°-x |
(3)∵BM⊥x轴,点B(2,4),
∴OM=2,BM=4,
∴MN=4,
∴MN=2OM,
∴∠ONM=30°,
∴∠OMN=90°-30°=60°,
∵MN=BM,
∴∠MNB=
| 1 |
| 2 |
∵∠MNP=∠MPN,
∴∠MNP=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BNP=∠MNB-∠MNP=75°-30°=45°.
点评:本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,等腰三角形的性质,难点在于(2)判断出∠BAD=45°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知关于x的方程ax2+bx+c=0(a≠0)的一个根是-1,则代数式
的值等于( )
| b-c |
| a |
| A、1 | B、-1 | C、-2 | D、2 |
计算(-3)0的结果是( )
| A、-1 | B、1 | C、0 | D、-3 |
 如图所示,一座拱桥的纵截面是抛物线的一段,已知拱桥的跨度是8米,水面宽6米时,水深3.5米,若水面宽5米,水有多深?
如图所示,一座拱桥的纵截面是抛物线的一段,已知拱桥的跨度是8米,水面宽6米时,水深3.5米,若水面宽5米,水有多深?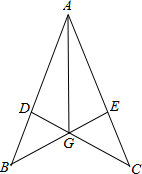 如图所示,BE⊥AC,CD⊥AB,BE、CD交于点G,且BG=GC,求证:∠BAG=∠CAG.
如图所示,BE⊥AC,CD⊥AB,BE、CD交于点G,且BG=GC,求证:∠BAG=∠CAG.