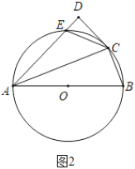
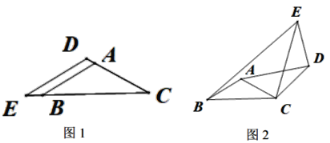
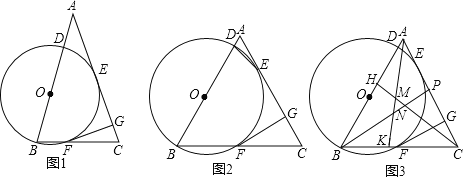
��Ŀ����
����Ŀ����ͼ1����������ȫ��ͬ��������ֽƬ![]() ��
��![]() �غϷ��ã�����
�غϷ��ã�����![]() ��
��![]() ��
��
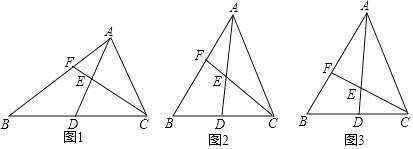
��1����������
��ͼ2���̶�![]() ��ʹ
��ʹ![]() �Ƶ�
�Ƶ�![]() ��ת������
��ת������![]() ǡ������
ǡ������![]() ����ʱ����գ�
����ʱ����գ�
���߶�![]() ��
��![]() ��λ�ù�ϵ��______��
��λ�ù�ϵ��______��
����![]() �����Ϊ
�����Ϊ![]() ��
��![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��
��![]() ��������ϵ��______
��������ϵ��______
��2��������֤
��![]() �Ƶ�
�Ƶ�![]() ��ת����ͼ3��ʾ��λ��ʱ��С������1����
��ת����ͼ3��ʾ��λ��ʱ��С������1����![]() ��
��![]() ��������ϵ��Ȼ�����������Էֱ�������
��������ϵ��Ȼ�����������Էֱ�������![]() ��
��![]() ��
��![]() ��
��![]() ���ϵĸߣ�����֤��С���IJ��룮
���ϵĸߣ�����֤��С���IJ��룮
��3����չ̽��
��֪��ABC=60�㣬��![]() �ǽ�ƽ������һ�㣬
�ǽ�ƽ������һ�㣬![]() ��
��![]() ��
��![]() �ڵ�
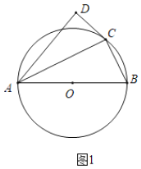
�ڵ�![]() (��ͼ4)����������
(��ͼ4)����������![]() �ϴ��ڵ�
�ϴ��ڵ�![]() ��ʹ
��ʹ![]() ���������Ӧ��
���������Ӧ��![]() �ij���
�ij���
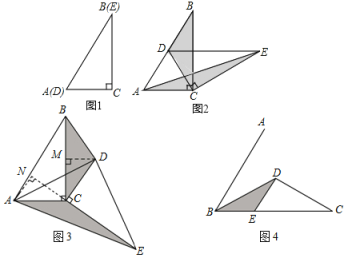
���𰸡���1���������֣���DE��AC����![]() =
=![]() ����2��������֤��
����2��������֤��![]() =
=![]() ��Ȼ������֤������������3����չ̽����
��Ȼ������֤������������3����չ̽����![]() =
=![]() ��
��![]()
��������
��1���������֣��ٸ���ֱ�������ε����ʼ��������EDC��Ȼ��֤����CADΪ�ȱ������οɵá�DCA=60�㣬�Ӷ��ó���EDC=��DCA��Ȼ�����ƽ���ߵ��ж����ɵó����ۣ�
�ڸ���ƽ����֮��ľ��봦����Ⱥ�ͬ�ȸ߿ɵ�S��DAC=![]() ��Ȼ�����30�����Ե�ֱ�DZ���б�ߵ�һ��͵ȱ������ε����ʿɵõ�DΪAB���е㣬�Ӷ�֤��S��DAC=
��Ȼ�����30�����Ե�ֱ�DZ���б�ߵ�һ��͵ȱ������ε����ʿɵõ�DΪAB���е㣬�Ӷ�֤��S��DAC=![]() �����ɵó����ۣ�
�����ɵó����ۣ�
��2��������֤������AAS֤����ACN�ա�DCM�����ɵó�AN=DM��Ȼ�������ת�����ʿɵ�EC=BC��Ȼ��������������εȵȸ��ɵó����ۣ�
��3����չ̽�����ӳ�CD��AB�ڵ�H������E��EG��BD��G������30�����Ե�ֱ�DZ���б�ߵ�һ����ɶ����ֱ����BH��GE��Ȼ����ݵ�F��λ�÷������ۣ��������������ε������ȡ��������ô��Ҳ��ȼ������FH���Ӷ��ֱ����BF�ij�
�⣺��1���������֣���DE��AC���������£�
��![]() ��
��![]() ��
��
���BAC=90�㣭��B=60�㣬��EDC=90�㣭��DEC=60��
�ߵ�![]() ǡ������
ǡ������![]() ����ʱ��
����ʱ��
��CA=CD
���CADΪ�ȱ�������
���DCA=60��
���EDC=��DCA
��DE��AC
�ʴ�Ϊ��DE��AC��
��![]() =
=![]() ����������
����������
��DE��AC
����ƽ����֮��ľ��봦�����
��S��DAC=![]()
��Rt��ABC����B=30��
��AB=2AC
�ߡ�CADΪ�ȱ�������
��AC=AD
��AB=2AD
���DΪAB���е�
��S��DAC=![]()
��![]() =
=![]()
�ʴ�Ϊ��![]() =
=![]() ��
��
��2��������֤��![]() =
=![]() ��Ȼ������֤������
��Ȼ������֤������
��AN��DM�ֱ��ǡ�ACE����BCD���ϵĸ�
���ANC=��DMC=90��
�ߡ�ACN����NCB=90�㣬��DCM����NCB=90��
���ACN=��DCM
�ڡ�ACN�͡�DCM��
���ACN�ա�DCM
��AN=DM
��EC=BC
���ACE�͡�BCD�ȵȸ�
��![]() =
=![]()
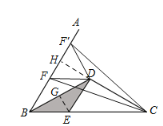
��3����չ̽�����ӳ�CD��AB�ڵ�H������E��EG��BD��G��
�ߡ�ABC=60�㣬��![]() �ǽ�ƽ������һ�㣬
�ǽ�ƽ������һ�㣬![]() ��
��
���HBD=��CBD=![]() ��ABC=30��
��ABC=30��
��![]()
���DCB=��DBC=30��
���BHC=180�㣭��HBC����DCB=90��
��Rt��BDH��HD=![]() ��BH=
��BH=![]()
��![]()
���EDB=��HBD=30��
���EBD=��EDB
��EB=ED
��BG=![]() =2
=2
��Rt��BEG����GE=x��BE=2GE=2x
���ݹ��ɶ����ɵã�GE2��BG2=BE2
��x 2��22=��2x��2
��ã�x=![]()
��GE=![]()
��i������F���߶�BH��ʱ��
��![]() ��
��![]()
��FH=GE=![]()
��BF=BH��FH=![]() ��
��
��ii����![]() ���߶�BH���ӳ�����ʱ
���߶�BH���ӳ�����ʱ
ͬ���ɵ�![]() H= GE=
H= GE=![]()
��B![]() =BH��
=BH��![]() H=
H=![]()
����������![]() =
=![]() ��
��![]()

 ���ѵ����Ԫ��ĩ���100��ϵ�д�
���ѵ����Ԫ��ĩ���100��ϵ�д� ��˼άС�ھ�100����ҵ��ϵ�д�
��˼άС�ھ�100����ҵ��ϵ�д� ��ʦָ��һ��ͨϵ�д�
��ʦָ��һ��ͨϵ�д�